You are viewing the documentation for an older COMSOL version. The latest version is
available here.
For a matrix material described by a Linear Elastic or Nonlinear Elastic materials, a Fiber described by a
Linear Elastic material adds a contribution to the stress tensor of the type
Here, Efib − E is the difference between the stiffness of the isotropic matrix
E and the fibers’ stiffness
Efib,
vfib is the fiber volume fraction,
a is the direction vector for the fiber orientation in the undeformed geometry, and
εa = a ·
εel ·
a is the elastic strain in the fiber direction
a.
For Nonlinear Elastic Materials, the same contribution to the stress tensor is added, although the stress-strain relation in the isotropic matrix could be nonlinear.
When the fiber stiffness is described by a Uniaxial stress function, the added stiffness reads
where σa(εa) is a function of the elastic strain in the fiber direction,
εa = a ·
εel ·
a. A linear elastic fiber can be described by
but in general, σa(εa) could be a nonlinear expression of the fiber strain
εa.
For Hyperelastic Materials, the
Holzapfel–Gasser–Ogden model is available beside the
Linear elastic and
Uniaxial data models for fibers. In this case, the fibers are represented by additional contributions to the strain energy density (
Ref. 29 and
Ref. 30).
Here, Wiso is the strain energy density of the isotropic hyperelastic material. In
Ref. 29 Wiso is represented by a nearly incompressible
Neo-Hookean material; in COMSOL Multiphysics it is possible to select any of the built-in hyperelastic material models.
The second and third terms, Wfib,1 and
Wfib,2 are anisotropic additions that describe the mechanical contribution of collagen fiber networks. These terms contribute with a strain energy density of the type
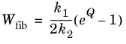 where
where 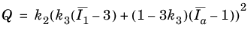
where the parameter k1 represents the fiber stiffness (SI unit: Pa),
k2 is a dimensionless tuning parameter, and
k3 is the fiber dispersion (dimensionless). A value of
k3 = 0 recovers the formulation in
Ref. 29, where all the fibers are perfectly oriented in the
a direction. Setting
k3 = 1/3 means that the fibers are completely dispersed, thus recovering a similar formulation as given in the
Delfino material model.
The invariant 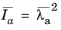 represents the squared value of the isochoric elastic stretch in the fiber direction a
represents the squared value of the isochoric elastic stretch in the fiber direction a. A common modeling assumption for biological tissues is that fibers cannot sustain compression, so the fiber stiffness is added only for tensile stretches such as
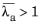
.
The hyperelastic formulation in the Holzapfel–Gasser–Ogden constitutive model (Ref. 29 and
Ref. 30) based on the isochoric elastic Cauchy–Green tensor can be problematic when the matrix material is made of a compressible or nearly incompressible material (
Ref. 31 and
Ref. 32).
The solution to this problem (Ref. 32) is to relax the isochoric restriction for the fiber deformation, and use the total strain invariant in the fiber direction instead. The contribution to the strain energy density then reads
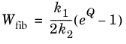 where
where 
The anisotropic strain energy density for the fiber family Wfib can also be specified as a user-defined expression of the strain invariants
Ia,
Ib,
Ic,
Iab,
Iac, and
Ibc, where
here, b and
c are orthogonal directions to the main fiber direction
a.
|
|
The internal variables Ia, Ib, Ic, Iab, Iac, Ibc, 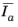 , 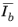 ,  , 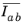 , 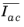 , and 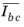 are named item.IaCe, item.IbCe, item.IcCe, item.IabCe, item.IacCe, item.IbcCe, item.IaCIe, item.IbCIe, item.IcCIe, item.IabCIe, item.IacCIe, and item.IbcCIe, respectively. Here, item is the name of the Fiber node (for instance, solid.hmm1.fib1).
|
where Efib − E is the difference between the stiffness of the isotropic matrix
E and the fibers’ stiffness
Efib,
vfib is the fiber volume fraction,
a is the direction vector for the fiber orientation in the undeformed geometry, and
εa = a ⋅ εel ⋅ a is the elastic strain in the fiber direction
a.
where εth,fib is the thermal strain in the fibers. When the fiber stiffness is described by a
Uniaxial stress function, the added stiffness reads
where σa(εa) is a function of the elastic strain in the fiber direction, where
For Nonlinear Elastic Materials, the same contribution to the stress tensor is added, although the stress-strain relation in the isotropic matrix could be nonlinear.
For Hyperelastic Materials containing one fiber family, the anisotropic strain energy density reads:
When Thermal Expansion is added to fibers described by the
Holzapfel–Gasser–Ogden material model, the fiber contribution
Wfib to the strain energy density is computed from the invariants of the elastic Cauchy-Green tensor:
The thermal strain in the fibers, εth,fib, can be specified by different means. When the secant coefficient of thermal expansion is used, it reads
Here, the secant coefficient of thermal expansion αs can be temperature-dependent. The reference temperature
Tref is the temperature at which there are no thermal strains in the fibers, and
Tfib is the current fiber temperature.