Tunneling
Equation 3-37 in the section Electrons in a Perturbed Periodic Potential describes the transport of both electrons and holes in a semiconductor with a potential that varies in space. In many circumstances the potential varies slowly in space and wave packets move according to the classical Hamiltonian, so correspondingly their dynamics is determined by the semiclassical model, from which both drift–diffusion equations follow. However, since Equation 3-37 is essentially a Schrödinger equation for electrons and holes, it allows for quantum mechanical phenomena such as tunneling, which are outside of the scope of the semiclassical model.
Tunneling occurs when an electron or hole wave packet is incident on a narrow potential barrier with a barrier height greater than the energy associated with the group velocity of the wave packet. A classical particle would be reflected at the boundary, but in the solutions of the Schrödinger equation the envelope function Ψm(r) associated with the wave packet decays exponentially inside the barrier. For thin barriers, Ψm(r) is significant on the opposite side of the barrier, and correspondingly there is a transmission probability associated with transport through the potential barrier. Since the tunneling probability must be computed for wave packets with a range of energies or k-vectors, it is usually only possible to solve the tunneling problem in 1D. Consequently, the approaches adopted are necessarily phenomenological in nature. The nature of the approximations required to arrive at the theory of tunneling is discussed in detail in section 4 of Ref. 42. Since much of the underlying theory is approximate in nature, it is sensible to favor numerically lighter solutions over more detailed approaches.
Tunneling commonly occurs in semiconductor devices at a variety of locations, including:
•
Tunneling through the barrier formed at a Schottky diode when the semiconductor is heavily doped underneath the metal contact (this is one way to produce an ohmic contact).
•
Tunneling through the potential barrier formed by the depletion layer associated with a heterojunction.
•
Direct tunneling through thin layers of oxide in very thin gates.
•
Tunneling into the conduction band of an oxide material when a high bias is applied to a thicker gate oxide (Fowler–Nordheim tunneling).
Note that for tunneling through direct band gap oxide barriers (such as silicon oxide) in indirect band gap semiconductors (such as silicon), an additional complication is encountered due to the band structure mismatch that occurs as a result of the change in the material at the interface. This mismatch is not usually observed in practice — for reasons that are currently not fully understood (see the discussion in chapter 5 of Ref. 45). In this case the phenomenological perspective adopted in Ref. 42 is usually employed, and tunneling through the barrier is treated without accounting for the band structure mismatch, since this approach best describes the experimental results.
In COMSOL Multiphysics, features enabling the modeling of Fowler–Nordheim tunneling are available.
Fowler–Nordheim Tunneling
When large fields are applied across an oxide layer, tunneling can occur directly into the conduction band of the oxide, as shown in Figure 3-17 below.
Figure 3-17: Band diagrams showing Fowler–Nordheim electron tunneling into the conduction band of an oxide. Eg is the band gap of the semiconductor, χ. is the electron affinity and Φm is the work function of the metal. The energy of the conduction band edge in the semiconductor is Ec, that of the valence band edge is Ev, the vacuum level is E0 and the Fermi level is Ef. In both (a) and (b) the temperature of the device is the same as the equilibrium reference temperature (temperature changes would cause an additional shift in the Fermi-level which are not shown in the figure - see for example, Figure 3-15). In (a) a large potential V0 is applied to the semiconductor. The band structure of the insulator is such that electrons can tunnel through the triangular barrier formed by the conduction band edge in the insulator, into the insulator conduction band. In (b) the potential V0 is applied to the metal, and consequently electrons from the metal can tunnel into the insulator conduction band. Once the electrons tunnel into the conduction band of the insulator they are transported via drift diffusion into the metal (case (a)) or semiconductor (case (b)). Note that the tunnel barrier presented to the electrons is triangular in shape in both cases.
Fowler and Nordheim originally treated tunneling through triangular barriers (Ref. 43) in the context of the Sommerfeld model. Their analysis was applied to tunneling in oxides within a semiconductor device context by Lenzlinger and Snow (Ref. 44). It is worth noting that Fowler and Nordheim did not make a WKB approximation in their original analysis, but instead approximated the final form of the analytic solution (a WKB approximation was used in Ref. 44 but for this reason is not strictly necessary). 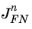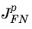The original result due to Fowler and Nordheim showed that the tunnel current through a triangular barrier for electrons () and/or holes () takes the form:
(3-148)
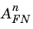
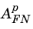
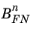
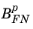
where Eins is the electric field in the insulator and , , , and are constants related to the material properties of the insulator and semiconductor. For the commonly encountered case of the silicon/silicon oxide system, only electron tunneling needs to be considered because the barrier for hole tunneling is significantly higher than that for electrons.
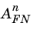
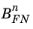
Ref. 44 provides a detailed derivation of Equation 3-148, for the case of a semiconductor–oxide system at finite temperature. The effect of a finite temperature was shown to be equivalent to a change in the values of the constants and . Similarly image force lowering effects at the barrier also caused an effective change in these constants. 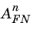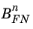Since using the derivative material properties does not lead to a fully consistent description of the tunneling current as a function of both electric field and temperature, it is customary to simply treat and as inputs to a model of the tunneling process at a particular temperature. These values can be extracted from a plot of log(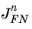/Eins2) versus 1/Eins.