where 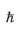is Planck’s constant divided by 2π and m is the electron mass. The time-independent Schrödinger equation takes the form of an eigenvalue equation. The modulus squared of the (complex) eigenfunctions (ψ) or wave functions that solve the equation represent the probability that an electron in the corresponding state can be found at a given position p(r) (that is, p(r) = ⏐ψ⏐2). The corresponding eigenvalue E for the state gives the energy associated with the state. For a detailed introduction to quantum mechanics see Ref. 7 and Ref. 8.

Since it is expected that the solid is periodic, the equation is solved on a cube of side L assuming the periodic boundary condition:

The solutions of Equation 3-1 and Equation 3-2 are plane waves of the form:

where Ω = L3 is the volume of the solid (which appears in the equation to correctly normalize the wave function) and:

where nx, ny, and nz are integers.

Since these states are all periodic, it is convenient to label them by means of the wave number k. Think of a k-space populated by these states in a regular cubic grid. As a consequence of the Pauli exclusion principle, each state can hold two electrons (one spin up and one spin down).

The density of states (g(k) = dns/ dξk), that is, the number of states (ns) per unit volume of k-space (ξk) for unit volume of the material, is given by:

Substituting Equation 3-3 into Equation 3-1 gives the energy of the particle in a given state:

At zero temperature electrons fill up the states with the lowest energy first, filling the grid so as to minimize the total energy. The surface dividing the filled states from the empty states — known as the Fermi surface — is spherical for large numbers of electrons as a result of Equation 3-4. For an electron number density n at zero temperature the magnitude of the wave vector corresponding to the states at the Fermi surface (kF,0) is given by:

At finite temperatures and at equilibrium, the principles of statistical mechanics (see for example Ref. 10) give the mean occupancy of the states (f0 (k)) as:

where EF is the Fermi energy or the chemical potential. At finite temperatures EF is determined by the requirement that the total number of electrons per unit volume is equal to n:

where g(E) = dns/ dE is the energy density of states, given by:

In deriving Equation 3-7, the E–k relationship (Equation 3-4) was used to evaluate the derivative and to convert from k to E.

These results form the basis of the Sommerfeld model and are useful in this discussion. Using this simple model, you can predict the thermal and electrical properties of some metals with reasonable accuracy (see Ref. 1 and Ref. 2 for details). However, the model does not explain the existence of insulators or semiconductors because it is missing important information about the microscopic periodicity of the material. The Effect of Periodicity section describes how this periodicity can be treated.