The energy equation for an incompressible fluid flowing in a pipe is (Ref. 25):

where ρ is the fluid density (SI unit: kg/m3), A is the pipe cross section area (SI unit: m2) available for flow, Cp (SI unit: J/(kg·K)) is the heat capacity at constant pressure, T (SI unit: K) is the temperature. u is a velocity field. For information about the tangential velocity in pipe flow, see Theory for the Pipe Flow Interface. Further, k (SI unit: W/(m·K)) is the thermal conductivity. The second term on the right hand side corresponds to friction heat dissipated due to viscous shear. Q (SI unit: W/m) represents a general heat source and Qwall (SI unit: W/m) represents external heat exchange through the pipe wall. Note that the Qwall term is detailed below.

An additional term Qp can be added to the right-hand side of the equation by enabling the Pressure Work check box:

This term is optional and can be used if the pressure drop is expected to be considerable and the fluid is compressible. The contribution follows the same theory as the pressure work term described in the section The Nonisothermal Flow and Conjugate Heat Transfer Equations in the Heat Transfer Module User’s Guide.

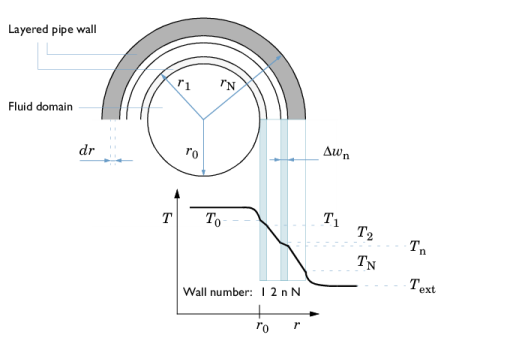
In Equation 3-3, (hZ)eff is an effective value of the heat transfer coefficient h (SI unit: W/(m2·K)) times the wall perimeter Z (SI unit: m) of the pipe. Text (SI unit: K) the external temperature outside of the pipe. See Figure 3-5. Qwall appears as a source term in the pipe heat transfer equation, Equation 3-1.

Text in Equation 3-3 can be a constant, parameter, or expression. Effective value of the heat transfer coefficient (hZ)eff is automatically calculated through film resistances and wall layers that are added as subnodes; see Equation 3-16.

If external temperature is computed by 3D Heat Transfer interface, add a Pipe Wall Heat Transfer coupling. The temperature coupling between the pipe and the surrounding domain is implemented as a line heat source in the 3D domain. The source strength is proportional to the temperature difference (Equation 3-3) between the pipe fluid and the surrounding domain.

The overall heat transfer coefficient including internal film resistance, wall resistance and external film resistance can be deduced as follows, with reference to Figure 3-5.

In Figure 3-5, consider a short length section ΔL of pipe, perpendicular to the figure plane. The heat leaving the internal fluid of that segment into the wall is

Here, AQ =  ΔL2πr0 (SI unit: m2) is the area available for heat flux into the wall. For stationary conditions that same amount of heat must travel through any cylindrical shell at radius r in wall 1 (or any wall).

Rearrange and integrate from r0 to r1.

and making a linear combination of the equations Equation 3-9 gives

where (hAQ)eff is an effective conductance:

For the general case with N wall layers this reads

where Z (SI unit: m) is an average perimeter (circumference), of the pipe, taken over the thickness of the pipe walls. Combine Equation 3-10 and Equation 3-14 such a that

and insert in Equation 3-13:

For a circular pipe cross sections, this effective hZ in can now be used in Equation 3-3. Note the reversed sign since Qwall is the heat added to the pipe from the surroundings. The assumptions in the deduction above are:

For square and rectangular pipe shapes the average conductance can be approximated by the simpler sum of resistances across a plane wall, which can be found in for example (Ref. 14):

where k is the thermal conductivity of the material, and Nu is the Nusselt number. dh is the hydraulic diameter, defined as

The local temperatures in each radial position of the pipe wall (see Figure 3-5) are computed considering the fact that Equation 3-3 also can be applied for each individual wall layer:

Combining Equation 3-3, Equation 3-19 and Equation 3-15 or Equation 3-16 (depending on pipe shape) for each wall layer explicitly gives each Tn.

For internal laminar forced convection in fully developed pipe flow, the Nusselt number is a constant that depends on the pipe cross-section. Values are listed in the table below (Ref. 1). The Pipe Flow interface interpolates to find values for width/height ratios not listed. Default settings for film coefficient calculations are “Automatic”, which means that laminar and turbulent correlations are applied according to the Re number.

For user-defined cross sections, Nu is suggested to 3.66 as a default.

For internal turbulent forced convection (3000 < Re <  6·106, 0.5 < Pr <  2000), the Gnielinski equation (Ref. 19) applies:

The film resistance due in the internal flow can be calculated using material properties defined in the Heat Transfer feature and the calculated friction factor. Material properties are evaluated at the mean internal film temperature (T + T0)/2 (see Expressions for the Darcy Friction Factor).

For External forced convection around a pipe, valid for all Re and for Pr > 0.2, the Churchill and Bernstein (Ref. 20) correlation is used:

For External natural convection around a pipe, the Churchill and Chu (Ref. 21) correlation is used which is recommend for Ra < 1012:

Above d is the outside diameter of the pipe and, β is the fluid’s coefficient of volumetric thermal expansion:

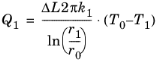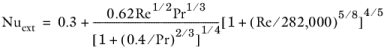Material properties are evaluated at (TN + Text)/2.