Droplet Breakup Theory
It is possible to model the breakup of liquid droplets using the Droplet Breakup feature. This feature supports two subfeatures, Kelvin–Helmholtz Breakup Model (added by default) and Rayleigh–Taylor Breakup Model, which correspond to different mechanisms for breakup. It is possible to include either breakup model separately or to use both models at once.
Dimensionless Numbers
When analyzing the mechanisms of droplet breakup, several dimensionless parameters are useful. These parameters are summarized in Table 5-3.
Table 5-3: Dimensionless Quantities Used in Droplet Breakup Models.
Symbol
Name
Expression
 Weg
Gas Weber number
 Wel
Liquid Weber number
 Rel
Droplet Reynolds number
 Z
Ohnesorge number
 T
Taylor number
where
•
ρ (SI unit: kg/m3) is the gas density,
•
ρp (SI unit: kg/m3) is the droplet density,
•
Urel (SI unit: m/s) is the relative speed between the droplet and gas,
•
rp (SI unit: m) is the droplet radius,
•
σp (SI unit: N/m) is the surface tension, and
•
μp (SI unit: Pa·s)is the droplet dynamic viscosity.
Kelvin–Helmholtz Breakup
The Kelvin–Helmholtz Breakup Model is based on a first-order linear analysis of Kelvin–Helmholtz instability in a cylindrical jet of fluid. For a parent droplet of radius r0 (SI unit: m), the wavelength ΛKH (SI unit: m) of the fastest-growing disturbance on the surface of the particle is
The corresponding growth rate ΩKH (SI unit: 1/s) of the fastest-growing disturbance is
The characteristic breakup time τKH (SI unit: s) can be derived from the wavelength and frequency of the fastest-growing disturbance,
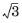
where BKH is a dimensionless constant. The value of BKH can vary considerably, depending on the mechanism for spray formation. Typical values are between and 60.
Kelvin–Helmholtz breakup is likely to occur when the parent droplet is sufficiently large and the time since previous breakup is comparable to or greater than τKH. The approximate size of the parent droplet over time is computed by allocating an effective Kelvin–Helmholtz radius rKH (SI unit: m) as an auxiliary dependent variable for all particles. The effective radius is initially equal to the parent droplet radius r0 and decreases over time according to the expression
Where rch (SI unit: m) is the child droplet radius,
where B0 = 0.61 is a dimensionless constant.
The criterion for breakup is that, at a time step taken by the solver, there exists a positive integer nch such that
When this criterion is true, a number of child droplets equal to nch is released at the parent droplet’s position. The new mass of the parent droplet mnew (SI unit: kg) is
Rayleigh–Taylor Breakup
The Rayleigh–Taylor Breakup Model is a significant breakup mechanism for droplets that undergo rapid accelerations. Compared to the Kelvin–Helmholtz model, in which child droplets are continually stripped away from a liquid jet, the Rayleigh–Taylor model describes the complete annihilation of the parent droplet as it breaks into a large number of child droplets.
According to the Rayleigh–Taylor model, a droplet breaks up when the wavelength of a disturbance on the droplet’s surface exceeds a critical value, which depends on the droplet’s radius.
Following Ref. 30, the wavelength of the fastest-growing disturbance ΛRT (SI unit: m) is
The frequency of the fastest-growing wave ΩRT (SI unit: 1/s) is
where a (SI unit: m/s2) is the magnitude of the droplet acceleration. The time constant for breakup τRT (SI unit: s) is
The radius of the child droplets rch (SI unit: m) is
where CRT is a dimensionless constant, with typical values ranging from 2.5 to 5.
When the Rayleigh–Taylor model is used, the time since previous Rayleigh–Taylor breakup tRT (SI unit: s) is defined as an auxiliary dependent variable for all particles. Whenever tRT > τRT at the beginning of a time step taken by the solver, the parent droplet is broken up into child droplets. The number of child droplets nch is
The floor operator is used to ensure that the number of child droplets is an integer, even though the resulting droplets may have radii different from rch.
Using Multiple Droplet Breakup Models
It is possible to include the Kelvin–Helmholtz and Rayleigh–Taylor breakup models in the same simulation. In this case, separate auxiliary dependent variables are allocated for the Kelvin–Helmholtz effective radius rKH and the time since previous Rayleigh–Taylor breakup tRT.
If the condition for Kelvin–Helmholtz breakup is met, then for the parent droplet and all child droplets tRT is set to zero.
If the condition for Rayleigh–Taylor breakup is met, then for all child droplets the Kelvin–Helmholtz radius rKH is set equal to the child droplet radius.