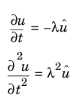When solving a PDE using an Eigenvalue study step, COMSOL Multiphysics assumes that all dependent variables vary with time as u(t) = ûe−λt, where û is a complex amplitude field. Therefore the time derivatives in Equation 16-1 and Equation 16-2 are interpreted as

Boundary conditions are treated as homogeneous for eigenvalue and eigenfrequency studies. It means, for example, that when using a Dirichlet boundary condition such as u = 7, it is treated as u = 0 when you use eigenvalue or eigenfrequency study steps. For nonlinear problems, the eigenvalue solver is linearizing the problem, including the constraints, around a linearization point for the dependent variables and an eigenvalue linearization point. For a nonlinear constraint (for u),

As an alternative to defining eigenvalue PDEs using the time-derivative coefficients ea and da, you can write the eigenvalue explicitly in the equations using the variable name lambda. For example, instead of specifying ea = 1, you can set a = lambda^2 with exactly the same result. In many cases, this formulation is preferable, in particular when the eigenvalue problem does not arise from a time derivative in a time-harmonic assumption.

The eigenvalue solvers solve eigenvalue problems that are at most quadratic polynomials in the eigenvalue lambda exactly in one step. Therefore, damped eigenvalue solutions are easily found when both ea and da are nonzero. Using the variable lambda, more complicated eigenvalue problems can be specified. Such problems must be solved using an iterative procedure.

Each time you run the eigenvalue solver, the PDE is expanded in a Taylor series in lambda around the eigenvalue linearization point λ0. Only the linear and quadratic terms are retained, while higher order terms are dropped. Running the solver repeatedly, updating the eigenvalue linearization point to the last eigenvalue found, usually converges to an eigenvalue solving the full nonlinear eigenvalue problem.