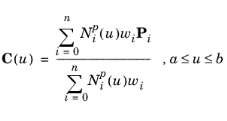The BSplineCurve describes a general spline curve using B-spline basis functions. Splines on this form are often referred to as B-splines.
A pth-degree spline curve is defined by
where Pi are the control points., the
wi are the weights, and the
Nip are the
pth degree B-spline basis functions defined in the nonperiodic and nonuniform knot vector
For Nip(u), the following definition is used:
The homogeneous control points Pw[i] used in the serialization of a rational curve have the components: