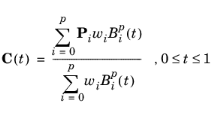are the Bernstein basis functions of
degree p,
Pi = ( x1, …,
xd) are the control points in the
d-dimensional space, and
wi are the weights, which should always be positive real numbers to get a properly defined rational Bézier curve. A rational Bézier curve has a direction defined by the parameter
t. The homogeneous control points
Pw[i] used in the serialization of a rational curve have the components: