Here ρi is the density, and xi the mole fraction of species i. Using the definition of the species density and mole fraction

Equation 3-55 can be expressed in terms of the mass fractions (ωi) in the manner of

Using Equation 3-55 together with the Maxwell–Stefan equations, where isobaric and isothermal conditions have been assumed, the following expression for the mixture-averaged diffusion coefficients can be derived (Ref. 3):

For this assumption, using Equation 3-57 together with the Maxwell–Stefan equations, also assuming isobaric and isothermal conditions, the following expression for the mixture-averaged diffusion coefficients can be derived (Ref. 3):

When using the mixture-averaged model, the diffusion is proportional to a single diffusion coefficient. The coefficient describes the diffusion of species i relative to the remaining mixture and is referred to as the mixture-averaged diffusion coefficient. The coefficient is explicitly given in terms of the multicomponent Maxwell–Stefan diffusivities Dik. As a consequence, no matrix inversion operation is required as for the Maxwell–Stefan diffusion model (when using four or more species). For low-density gas mixtures, the Dik components can be replaced by the binary diffusivities for the species pairs present.

It should be noted that models for the multicomponent diffusivities based on Fick’s law are approximations. One drawback of this is that the net diffusive mass flux, the sum of all mass fluxes relative to the mass averaged velocity, is not constrained to zero. To account for this we add a flux, defined by a correction velocity uc, to enforce a zero net diffusive flux in the manner of:

Here ud,i is the diffusion velocity resulting from the flux assumption in Equation 3-55 or Equation 3-57. Note that the correction velocity is a constant correction (same for all species), but varies in space.

Using the correction velocity together with Equation 3-55 (flux proportional to the mole fraction gradient), the resulting diffusive flux is

If instead Equation 3-57 is used (flux proportional to the mass fraction gradient), the resulting diffusive flux is

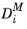
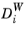
For the Fick’s law or the Mixture-averaged diffusion models, the diffusion coefficient is corrected with the Wall diffusion coefficient in the following way

For the Maxwell-Stefan diffusion model, the following term is added to the species force balance (Equation 3-46)

The wall velocity uW, representing the velocity of the fluid in a representative region adjacent to the pore wall, is here defined as

It should be noted that uW can become nonzero also in the absence of pressure gradients. For a proper description of the fluid momentum balance, uW needs to be added either as a contributing velocity (Darcy’s law) or as a corresponding volume force F = μκ−1uW (Brinkman equations).

The Maxwell–Stefan model formulated in this way correctly captures the Klinkenberg effect, and has large similarities with other models in literature incorporating Knudsen diffusion such as the Dusty Gas Model and the (Modified) Binary Friction Model. In addition, for the limit of vanishing permeabilities (κ → 0), the formulation reduces to the Lightfoot model for membrane transport.