Multicomponent Gas Diffusion: Maxwell–Stefan Description
The Maxwell–Stefan formulation for a multicomponent mixture defines N − 1 (with N being the number of active species in the model) force balances according to
(3-46)
where
•
Dik (SI unit: m2/s) are the binary Maxwell–Stefan diffusivities
•
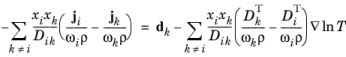
T (SI unit: K) is the temperature
•
(SI unit: kg/ m·s)) are the thermal diffusion coefficients, and
•
dk (SI unit: 1/m) is the diffusional driving force acting on species k.
By inverting the above set of equations, the mass flux relative to the mass average velocity, ji, can be defined by the generalized Fick equations (Ref. 1):
(3-47)
where (SI unit: m2/s) are the multicomponent Fick diffusivities.
For ideal gas mixtures the diffusional driving force is (Ref. 1)
(3-48)
where
•
c (SI unit: mol/m3) is the total molar concentration
•
Rg is the universal gas constant 8.314 J/(mol·K)
•
p (SI unit: Pa) is the total pressure
•
pk (SI unit: Pa) is the partial pressure, and
•
ρk (SI unit: kg/m3) is the density of species k, and
•
gk (SI unit: m/s2) is an external force (per unit mass) acting on species k. In the case of an ionic species the external force arises due to the electric field.
When an external force applies equally to all species (such as for gravity), the last two terms disappear.
As can be seen in Equation 3-47 and Equation 3-48, the total diffusive flux for the species depends on the gradients of all species concentrations, temperature, and pressure as well as any external force on the individual species.
Using the ideal gas law, p = c·Rg·T, and the definition of the partial pressures, pk = xkp, the equation can be written as
(3-49)
The mole fraction xk is given by
(3-50)
and the mean molar mass M (SI unit: kg/mol) by
When using the Maxwell–Stefan diffusion model, the transport equations for the species’ mass are
(3-51)