Equations for compressible turbulence are derived using the Favre average. The Favre average of a variable T is denoted and is defined by

With this notation the equation for total internal energy, e, becomes

where h is the enthalpy. The vector

is the laminar, viscous stress tensor. Notice that the thermal conductivity is denoted λ.

is modeled using the Boussinesq approximation:

where k is the turbulent kinetic energy, which in turn is defined by

The correlation between uj″ and h″ in Equation 4-5 is the turbulent transport of heat. It is modeled analogously to the laminar conductive heat flux

are modeled by a generalization of the molecular diffusion and turbulent transport terms found in the incompressible k equation

Inserting Equation 4-6 through Equation 4-10 into Equation 4-5 gives

The Favre average can also be applied to the momentum equation, which, using Equation 4-7, can be written

Taking the inner product between 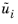and Equation 4-12 results in an equation for the resolved kinetic energy, which can be subtracted from Equation 4-11 with the following result:

According to Wilcox (Ref. 1), it is usually a good approximation to neglect the contributions of k for flows with Mach numbers up to the supersonic range. This gives the following approximation of Equation 4-13 is

Larsson (Ref. 2) suggests to make the split

Equation 4-15 is completely analogous to the laminar energy equation and can be expanded using the same theory (see for example Ref. 3):

This is a relatively exact model for PrT, while still quite simple. In Ref. 4, it is compared to other models for PrT and found to be a good approximation for most kinds of turbulent wall bounded flows except for turbulent flow of liquid metals. The model is given by

where the Prandtl number at infinity is PrT∞ = 0.85 and λ is the conductivity.

Weigand and others (Ref. 5) suggested an extension of Equation 4-16 to liquid metals by introducing

where Re∞, the Reynolds number at infinity, must be provided either as a constant or as a function of the flow field. You enter the Reynolds number in the Model Inputs section of the Fluid feature.

Both automatic wall treatment and wall functions introduce a theoretical gap between the solid wall and the computational domain for the fluid and temperature fields. See Wall Boundary Conditions described for The Algebraic yPlus Turbulence Model and The k-ε Turbulence Model). This theoretical gap applies also to the temperature fields but is most often ignored when the computational geometry is drawn.

The standard temperature wall function takes into account conduction in the boundary layer. The heat flux between the fluid with temperature Tf and a wall with temperature Tw, is

where ρ is the fluid density, Cp is the fluid heat capacity, and uτ is the friction velocity. T+ is the dimensionless temperature and is given by (Ref. 6)

λ is the thermal conductivity, and κ is the von Kármán constant equal to 0.41.

Variables with an index “c” are evaluated at the critical distance, which corresponds to the switch from the laminar sublayer to the logarithmic layer. The critical wall distance δw+c, which depends on the turbulent parameters κ and B, is estimated from a second-order accurate solution:

with κ0 = 0.41, B0 = 5.2, and X0 = 4.53554291157957.

The velocity at δw+c is then calculated from a velocity wall function, according to the turbulence model and wall treatment chosen to keep consistency. The velocity wall function used for the determination of Uc when the L-VEL or a LES turbulence model is chosen is based on a blending of the linear and logarithmic laws. It gives very similar results to the wall function actually used for the calculation of the velocity at the first cell which is based on the wall Reynolds number.

The distance between the computational fluid domain and the wall, δw, is always hw/2 for automatic wall treatment where hw is the height of the mesh cell adjacent to the wall. hw/2 is almost always very small compared to any geometrical quantity of interest, at least if a boundary layer mesh is used. For wall function, δw is at least hw/2 and can be bigger if necessary to keep δw+ higher than 11.06. The computational results should be checked so that the distance between the computational fluid domain and the wall, δw, is everywhere small compared to any geometrical quantity of interest. The distance δw is available for evaluation on boundaries.