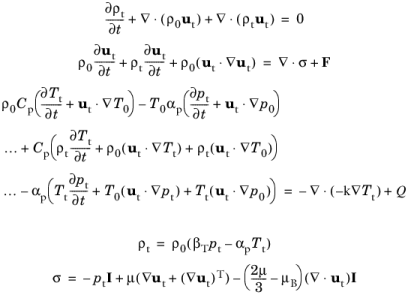The governing equations solved in a transient thermoviscous acoustics model that uses the Nonlinear Thermoviscous Acoustics Contributions feature are also derived from Equation 6-4 using a first order perturbation approach. However nonlinear terms in the perturbations are retained. This yields the set of nonlinear thermoviscous acoustics equations

In the default formulation only the linear equation of state is retained. This is a good approximation in most cases as cumulative nonlinear effects typically can be neglected in microacoustics. The nonlinear equations will capture local nonlinear effects like vortex shedding. These can occur when the linearity condition |ut| << c is no longer fulfilled. Note that the vortices are generated by the acoustic field itself.

In models with high local sound pressure levels, the linear equation of state may no longer be valid. This happens when the linearity condition on the density ρt << ρ0 is no longer fulfilled. If necessary, the feature has an option to change the default Density expansion from First order to Second order. This corresponds to the following second order equation of state

Additional inputs to the model are necessary. For the general case, the second order derivatives of the equilibrium density ρ0 = ρ0(p0,T0) with respect to pressure p0 and temperature T0 are needed. They contribute to the second-order Taylor expansion of the density. Per default, they are taken From equilibrium density; this implies that the dependency of the density on pressure and temperature should be correct and included. Note that this dependency is included if a material is defined using the functionality of the Liquid & Gas Properties Module (see the Material Properties section in the Acoustic Properties of Fluids chapter for details).