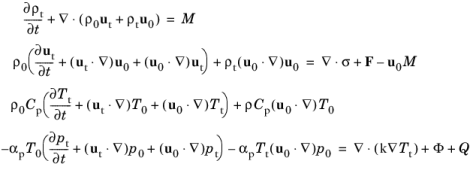
|
•
|
|
•
|
|
•
|
|
When modeling aeroacoustics, it is important how the Mapping Between Fluid Flow and Acoustics Mesh is done from a numerical perspective. The Background Fluid Flow Coupling multiphysics coupling handles this in an automated manner.
Physically the Coupling to Turbulent Flows (Eddy Viscosity) is also important to model the attenuation of acoustics waves due to turbulence.
|
|
Details about the Model Input and the Default Model Inputs are found in the Global and Local Definitions chapter of the COMSOL Multiphysics Reference Manual.
|
|
•
|
Background mean flow density ρ0(p0, T0) (SI unit: kg/m3). The Ideal gas option can also be selected as the density formulation.
|
|
•
|
|
•
|
|
•
|
Thermal conductivity k (SI unit: W/(m·K)).
|
|
•
|
|
•
|
For the From speed of sound (the default for both) options the values for the Speed of sound c0 (SI unit: m/s) and Ratio of specific heats γ (dimensionless) are taken From material. For User defined enter a different value or expression. The From speed of sound option is typically preferred (and the default) as the speed of sound and the ratio of specific heats are material properties often more readily available (see definition above).
|
|
•
|
For the From background mean flow density the values are computed from the density expression (see definition above). This option is only valid if the density material property has the built in dependency on pressure p0 and temperature T0. This is not always the case.
|
|
•
|
For From material, the coefficient of thermal expansion is taken from the materials node. Not all materials have this property defined. If this is the case a small warning cross will appear on the materials node.
|
|
•
|
For the From isentropic compressibility option, the values for the Isentropic compressibility βs (SI unit: 1/Pa) and Ratio of specific heats γ (dimensionless) are taken From material (the default). For User defined enter a different values or expressions.
|
|
•
|
For User defined enter a value or expression for the isobaric coefficient of thermal expansion αp (SI unit: 1/K) and/or the isothermal compressibility βT (SI unit: 1/Pa).
|