The Radiation Pattern plots are available with this module to plot the value of a global variable (for example, the far field norm, normEfar and normdBEfar, or components of the far-field variable Efar).

The variables are plotted for a selected number of angles on a unit circle (in 2D) or a unit sphere (in 3D). The angle interval and the number of angles can be manually specified. For 2D Radiation Pattern plots, the reference direction from which the angle is measured and the normal to the plane the far field is computed for can also be specified. For 3D Radiation Pattern plots, you also specify an expression for the surface color.

The main advantage with the Radiation Pattern plot, as compared to making a Line Graph, is that the unit circle or sphere that you use for defining the plot directions is not part of your geometry for the solution. Thus, the number of plotting directions is decoupled from the discretization of the solution domain.

1See Directivity via Global Evaluation.

2See 3D Far-Field Norm Functions in 2D Axisymmetry.

3See Array factor operators.

4See Far-Field Analysis Using Functions and Operators.

The postprocessing far-field functions are available under Component>Definitions>Functions. Below you find example models using these functions and some links to more information.

The functions norm3DEfar and normdB3DEfar calculate the 3D far-field norms, based on field solutions in 2D axisymmetric geometry. These functions are available in these cases:

The function can be used in a 3D Radiation Pattern plot, where the input argument of the function must be same as the Azimuth angle variable in the Evaluation section in the Settings window.

The suffix of a function name varies based on the circular port mode type, port mode number, and azimuthal mode number in the physics interface. For example, when using azimuthal mode number 1 in the physics interface and transverse electric (TE) mode with mode number 2 in the port settings, the generated operator name is norm3DEfar_TE12.

When the function is used in a radiation pattern plot under a 1D or a polar plot group, the value of input argument defines the plotting plane regardless of the normal and reference direction in the Evaluation section in the Settings window. For example, norm3DEfar_TE12(0)evaluates the norm of the electric far field for the TE12 mode for a 0-degree azimuthal angle. This is equivalent to plotting this variable on the xz-plane. Similarly, norm3DEfar_TE12(pi/2) is the evaluation at a 90-degree azimuthal angle, which is equivalent to plotting the variable on the yz-plane.

The equation for the uniform three dimensional array factor operator af3 is

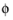
where θ is the elevation angle and is the azimuthal angle.

The uniform two-dimensional array factor operator af2 is simpler than the three-dimensional version, as the third, the z-component factor, is unity.

While plotting a 3D radiation pattern, the maximum directivity can be calculated by evaluating the ratio between the radiation intensity and the average value of the radiation intensity. Since the radiation intensity is a function of power, the square of the far-field norm has to be used in the Directivity expression in the Radiation Pattern settings window for the antenna directivity calculation. For other physics interfaces, such as in the Acoustics module, the expression is different.

The maximum directivity can be computed through Results>Derived Values>Global Evaluation. This calculation is based on the maximum and averaged intensity values on the far-field calculation selection. It requires the selection for the far-field calculation feature to be spherical for 3D and circular for 2D axisymmetric model components, both centered at the origin.

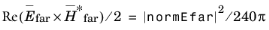
where U is the radiation intensity, , and Pin is the total input power.

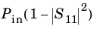
where the delivered power, Pdelivered is . The gain is available only when the S-parameter calculation is valid, that is, for the single port excitation case.