The Gaussian process (GP) model, also known as the Kriging model, is a popular surrogate model that gives an approximate prediction of the QoIs, is probabilistic, and computes the variance of the prediction at every sample point in the input parameter space. A GP is specified by its mean, also known as the trend, and a covariance function, also called a kernel or correlation function. The hyperparameters of the mean and covariance functions are optimized while training the GP model. Consider input parameters x and a scalar QoI y. The GP model can then be expressed as

where m(x) is the mean function and f(x) is a GP with zero mean and covariance kθ(x, x'). Here, θ represents the hyperparameters of the covariance function.

where f = y − m(x), y is the evaluated QoI, and f' and x' are the predicted QoI and its corresponding input parameters.

where μ(x) and cov(x, x') are the mean and covariance of the model, respectively:

and the Matérn class kernel with ν = 3/2 and ν = 5/2

where r is a function of x and x' defined as

Here, 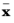is defined as 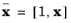and ∑ = diag(σ02, σ2), where σ0 and σ =  (σ1, …, σm) are the hyperparameters. Further details about the covariance function and the Gaussian process can be found in Ref. 7.

The covariance functions are assumed to be anisotropic. The automatic relevance determination (ARD) method is used to define different length scales for each input parameter. The ARD method is given its name because estimating the length scale parameters implicitly determines the “relevance” of each dimension. Input dimensions with relatively large length scales imply relatively little variation along those dimensions in the QoI function being modeled.

The spectral exponential kernel has strong smoothness where the Matérn kernel with ν = 5/2 is less smooth, and the Matérn kernel with ν = 3/2 is more rough. The GP model with a spectral exponential kernel is infinitely differentiable, whereas the GP model with a Matérn kernel is differentiable a finite number of times. Comparing the Matérn kernel and a spectral exponential kernel with the same length scale, the Matérn kernel has weaker correlation and is more oscillatory. Samples from a GP with the one-layer neural network kernel can be viewed as superpositions of functions with a single-layer neural network with erf(xT ∑ x') as the activation function. The GP model created with a single-layer neural network is smooth. In the region with a large absolute value of x, they approximate to a constant value.

Regardless of which covariance matrix is used, it is often the case that it needs to be inverted while training the GP model. The inversion is known to suffer from numerical instabilities. To circumvent such limitations, a nugget factor defined as σ2I is added to the covariance matrix. Here, σ is learned as an additional hyperparameter during the training of the GP.

If there is a priori information of the mean function, it can be used to increase the modeling accuracy. One example of using a mean function is that when a GP is used for sensitivity analysis and uncertainty propagation, the extrapolation of the GP far from the sample points might be computed. If there is a priori information of the mean, using a linear or quadratic mean function can be beneficial for the extrapolation.

Since the log-likelihood may have multiple local optima, the local optimizer for training the hyperparameters needs to be started repeatedly by specifying different starting points in the hyperparameter space. This surrogate model provides an automatic number of restart points for training the hyperparameters. These points are chosen such that they are in the regions where the hyperparameters render relatively small negative log-likelihood. Also, the restarting points are space filling in the hyperparameter space. These points are obtained by first generating a large amount of possible choices and then using a K-cluster mean method to select different starting points following the method described in Ref. 8 from the Journal of Statistical Software.

For adaptive GPs, the GP is constructed adaptively by adding a new input parameter point at the location of the maximum entropy, when it is used for sensitivity analysis or uncertainty propagation, or at the location of the maximum expected feasibility function, when it is used for reliability analysis. For sensitivity analysis or uncertainty propagation, the GP is trained to approximate the underlying model accurately in the entire input parameter space. It follows the heuristics in Ref. 9, which adds a new point at the location with the highest entropy. Here, the entropy is defined as the standard deviation of the GP model. For reliability analysis, the GP is trained to accurately approximate the underlying model only near the regions that satisfy the reliability conditions, where the maximum expected feasibility function is used to find the adaptation points. More details about the expected feasibility function can be found in Reliability Analysis — Efficient Global Reliability Analysis.

To explore the region in the input parameter space and exploit the most-recently-built GP, a global optimization problem is solved in every adaptation step in finding the location corresponding to the maximum entropy or maximum expected feasibility function. There are two types of global optimization methods, the dividing rectangles (DIRECT) method (see Ref. 10) and the Monte Carlo method. The default choice is the DIRECT method. For nonadaptive GPs, this global optimization procedure is used to determine the maximum entropy as the error estimation of the model. Note that nonadaptive GP models are not used for reliability analysis.