Reliability Analysis — Efficient Global Reliability Analysis
The goal of reliability analysis is to determine the probability that a model will satisfy certain criteria given by the user-defined threshold. Thus, the probability, pf, is defined by
where f(x) is the probability density function for the input parameters x, and the integration is performed over the region where the condition COND(y, z) is satisfied. Here, y is the vector of the QoIs, and z is the value of the threshold corresponding to each QoI.
For the jth QoI, the probability condition cond(yj, zj) is true if yj > zj or yj < zj.
For reliability analyses with multiple QoIs, the probability condition can be formed as “all true”, where the condition is defined as
or “any true” where the condition is defined as
where n is the number of QoIs. In general, this integration is impossible to obtain with analytical methods.
Therefore, the integration is approximated, for example, with Monte Carlo analysis. Note that when comparing existing local reliability analysis methods, numerical integration is generally more accurate but it requires a large number of function evaluations. Similar to surrogate-based sensitivity analysis and uncertainty propagation, the reliability analysis is built with the use of a surrogate model. It uses the efficient global reliability analysis (EGRA), which is built on an adaptive Gaussian process (GP). The method balances the exploration of the region where the GP provides a good prediction and exploitation of the region where the GP has large variance and more model evaluations are required. Furthermore, it does not require the GP model to have high accuracy in the region far from the limit state where the QoIs are equal to the thresholds. This is achieved by focusing on adding adaptive model evaluations around the limit state that reduces the number of model evaluations.
The expected feasibility function (EFF), which is used as the adaptive error estimation in EGRA, is used to select the location of the next input parameter point. The EFF defines the expectation of the sample lying within the vicinity, defined by ±ε(x), around the limit state. The feasibility function at x is defined as being positive within the vicinity around the limit state and 0 otherwise. For problems with a scalar value QoI y, the EFF is defined as the expectation of being within the vicinity around the limit state given by
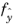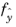
where is the probability of the AGP and y is realizations of . Note that ε defines the vicinity around z and is set to 2σy, where σy is the standard deviation of the AGP model.
Note that EFF provides a balance between exploration and exploitation: Points where the expected value is close to the threshold and points with a large uncertainty in the prediction will have a larger expected feasibility value. The adaptation point is defined as
The most efficient way of finding the solution to system-level EGRA problems is to construct a GP for each individual quantity of interest and then construct a composite EFF. Additional details about the EFF can be found in Ref. 13.
There are two sampling methods: One is to use importance sampling and the other is simply using Latin hypercube sampling. For the Lain hypercube sampling method, some number of samples of the input parameters are first randomly generated based on their distributions. Then, the surrogate models are evaluated at their input points. The values of the surrogate model at these points are compared with the threshold to determine if the predicted QoIs satisfy the probability conditions. The probability pf is then calculated as the ratio of the number of predicted QoIs that satisfy the criteria for the total number of samples:
Here, Nf is the number of predicted QoIs that satisfy the criteria, and N is the number of all samples. One drawback of this method is that the majority of the samples lie in the high-probability region of the input parameter space. If the region defined by the threshold is a low-probability region, a very large number of samples is required to ensure enough samples to be located in such a region. Another method is the multimodal adaptive importance sampling method, which combines the surrogate model and Latin hypercube sampling. Compared to the Latin hypercube method, the importance sampling method uses fewer samples and provides an error estimation.
The procedure of performing EGRA with importance sampling is as follows. First, an initial set of model evaluations is computed and the initial GP is constructed based on these data. Then the point with maximum expected feasibility is searched as a global optimization problem using the GP model. Next, the adaptation model evaluation is evaluated at the point, and the enhanced dataset is used to construct an updated GP. The adaptation procedure is repeated until the maximum expected feasibility is smaller than the relative tolerance or the maximum number of model evaluations is reached. The final GP provides information on the data points located near the limit state, which serves as a good initial state for the importance sampling method.
To ensure that the initial GP covers a sufficiently large region in the input parameter space, instead of sampling according to the input parameter distribution, the reliability analysis uniformly samples in the region between the minimum and maximum values of each input dimension where the minimum and maximum is user specified or given by the input parameter distribution and the lower and upper cumulative distribution function. Note that when the initial GP has too little information (too few model evaluations) or the global optimization does not cover a sufficiently large space, the EFF may not locate the limit state. Increasing the initial number of model evaluations and the maximum surrogate evaluations for optimizations for the global optimization procedure of finding maximum EFF could improve the accuracy of the analysis.