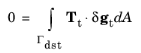You are viewing the documentation for an older COMSOL version. The latest version is
available here.
(3-185)
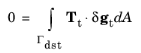
where Tt is the friction force. The stick and slip conditions are then enforced by the constitutive model used to define
Tt.
(3-186)
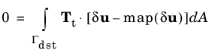
(3-187)
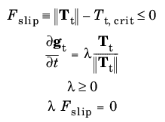
where Fslip is the slip function (analogue to the yield function in plasticity theory), and
λ is friction multiplier. The critical friction force
Tt,crit determines when slip occurs, and is defined as
where Tcohe is the cohesion, and
Tt,max defines the maximum friction force that is admissible. The friction coefficient
μ can either be defined as an arbitrary constant expression or through an exponential decay model in time-dependent studies. The latter model is defined as
where μstat is the static friction coefficient,
μdyn is the dynamic friction coefficient,
vs is the slip velocity, and
αdcf is a decay coefficient.
It is possible to also define the critical friction force through an arbitrary expression. In principle, Tt,crit, or any variable described above, may be defined as a function of any other variable or field. However, the implementation described in the following is only valid as long as it does not dependent on
Tt. In other words, the implementation of the friction constitutive model does not allow for hardening behavior of the friction force.
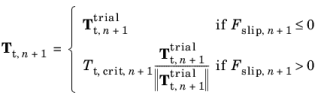
In COMSOL Multiphysics, implementation of Equation 3-187 is made using a backward Euler integration. Together with a penalty regularization, this results in the following set of algebraic equations to solve at increment
n+1:
where Tt,n is the friction force at the previous increment. The set of algebraic equations is solved for unknowns
Tt,n+1 and
λ by introducing a trial state and a return mapping. In doing so, it is assumed that
Tt,crit, n+1 is independent of
Tt, n+1, which leads to an explicit set of equations for finding
Tt, n+1. The trial state is first computed as
(3-188)
(3-189)
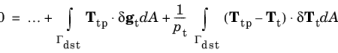
where Ttp is the penalized (or augmented) friction, and
Tt is a Lagrange multiplier that can be identified as a traction. Alternatively,
Equation 3-186 can be augmented, giving the following result
(3-190)
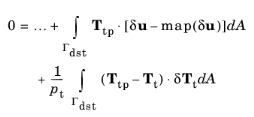
The Lagrange multiplier Tt is defined as the dependent variable of the contact problem and is typically discretized using Lagrange shape functions. There are two methods for solving the above coupled system of equations,
Segregated and
Fully coupled, as selected in the parent
Contact node.
As for the penalty method, Equation 3-187 is implemented using backward Euler integration of the evolution equations, and a trial state and return mapping to solve the nonlinear algebraic equations.
When the Segregated solution method is selected in the parent
Contact node, the trial state for outer iteration
j+1 is computed as
This scheme then fits in to the algorithmic format described for normal contact where the displacement field u and the Lagrange multipliers associated with contact are solved in a segregated way. Including friction, this algorithm is schematically described as
|
1
|
Initialize increment n+1 by setting the outer iteration counter j=0, and the initial values for dependent variables 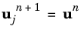 , 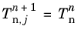 , and 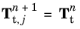
|
When the Fully coupled solution method is selected in the parent
Contact node, the trial friction force for iteration
i+1 is computed as
The definition of Tt is done in a similar way as for the penalty method following
Equation 3-188. However, for Nitsche’s formulation of frictional contact, the trial friction force is given as
where Tat is the tangential part of the nominal traction vector. Note that the same penalty factor,
pn, is always used for the normal and tangential parts of the contact problem when using the Nitsche method.
In the Slip Velocity subnode to
Contact, it is assumed the tangential contact is in a slip state when in contact, and that the relative motion between the source and destination boundaries is known beforehand. That is
where vslip is the prescribed velocity on the destination boundary relative to the source boundary. Given that the rate of the slip is known, the constitutive model for friction in
Equation 3-187 is simplified, and it follows that
Friction is a dissipative process and the accumulated dissipated energy Wfric can be computed by solving a distributed ODE on the destination boundary: