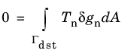You are viewing the documentation for an older COMSOL version. The latest version is
available here.
(3-176)
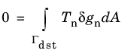
where Tn is the contact pressure, assumed positive in compression. To complete the contact condition,
Equation 3-176 is subjected to the Kuhn–Tucker conditions
(3-177)

where the first inequality represents the nonpenetration condition. Equation 3-176 and
Equation 3-177 together represents a unilateral constraint that require special techniques to implement. Several different techniques for doing so are available in COMSOL Multiphysics, which can be divided into two main classes: the
penalty method, the
augmented Lagrangian method, and the
Nitsche method.
(3-178)
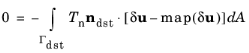
In principle, Equation 3-176 and
Equation 3-178 describes the same contribution to the virtual work. However, when the system of equations are linearized they will produce different results. The main difference originates from the variation
δgn with respect to
u that, for the ray-tracing mapping strategy used by COMSOL Multiphysics, includes several terms that can be difficult and expensive to evaluate. These are not present if
Equation 3-178 is used, which can increase the robustness of the solution. What formulation that is used can be controlled by the
Jacobian contribution setting in the
Contact node. When set to
Symmetric or
Legacy,
Equation 3-176 is used. For
Symmetric, some terms of
δgn are omitted to improve the robustness, whereas
Legacy uses the full variation of
δgn. When the
Nonsymmetric option is selected,
Equation 3-178 is used.
For the penalty method, the contact pressure in Equation 3-176 is represented using a penalization of the physical gap so that
(3-179)
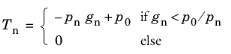
where pn is the penalty factor, and
p0 is the pressure at zero gap. This leads to an approximative solution of the nonpenetration condition. The penalty method as defined by
Equation 3-179 is conceptually based on the insertion of a nonlinear spring between the contacting points. The penalty factor can be interpreted as the stiffness of that spring. A high value of the stiffness enforces the contact conditions more strictly, but if it is too high, it makes the problem ill-conditioned and unstable.
The pressure at zero gap, p0, can be used to reduce the overclosure between the contacting boundaries if an estimate to the contact pressure is known. In the default case, when
p0 = 0, there must always be some overclosure in order for a contact pressure to develop.
In addition to Equation 3-179, COMSOL Multiphysics also provides an alternative penalization based on a viscous formulation intended for transient simulations, referred to as the
Penalty, dynamic method. This formulation is based on the additional persistency condition
(3-180)
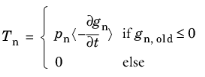
where gn,old is the physical gap distance at the previous increment, and <> is the positive parts operator. With the definition in
Equation 3-180,
Tn is only nonzero if the physical gap is negative during the entire increment, which is important for energy conservation during the initial contact event. However, there will always be some initial penetration before the gap rate is penalized. Hence the observed overclosure will be dependent on the size of the increment when two points come into contact. Note that this definition of the contact pressure implies that pressure contact is dissipative.
It is possible to use the definitions of Tn in
Equation 3-179 and
Equation 3-180 simultaneously. In such a case, they are additive and conceptually represent a parallel coupling of a spring and a dashpot.
(3-181)
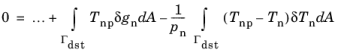
where Tnp is the penalized (or augmented) contact pressure, and
Tn is a Lagrange multiplier that can be identified as a contact pressure. Alternatively,
Equation 3-178 can be augmented, giving the following result
(3-182)
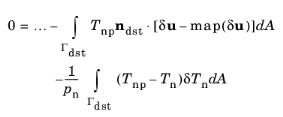
The Lagrange multiplier Tn is defined as a dependent variable of the contact problem and is typically discretized using Lagrange shape functions. There are two methods for solving the above coupled system of equations, and this choice affects the definition of
Tnp.
The first solution method is referred to as a Segregated method and corresponds to the so-called Uzawa algorithm. Here, the system of equations is decoupled, and the displacement field
u and the Lagrange multiplier
Tn are solved in a segregated way. This leads to two levels of iterations in the solver, where
Tn is held constant when solving for
u, and vice versa when updating
Tn. For this solution method, the penalized contact pressure
Tnp is defined with a smooth transition to stabilize the problem when transitioning between contact states. The definition for
Tnp for outer iteration
j+1 is defined by
|
1
|
Initialize increment n+1 by setting the outer iteration counter j=0, and the initial values for dependent variables 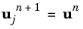 and 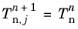
|
The appropriate solver sequence is automatically set up by COMSOL Multiphysics for the Segregated solution method when adding a new solver, or resetting to the default solver.
The alternative is to use a Fully Coupled solution method, which, as the name implies, amounts to solving the coupled system in
Equation 3-181 or
Equation 3-182 for the two dependent variables
u and
Tn (and any other variables included in the multiphysics model). When using this method, the penalized contact pressure is defined by
The Fully Coupled method can be convenient as it enforces the nonpenetration condition exactly over the contacting boundaries, while it puts no restriction on how to set up the solver sequence. This flexibility can be especially advantageous when working with multiphysics problems, compared to the segregated approach. However, one should be aware that the method comes with some of the drawbacks of a pure Lagrange multiplier approach, albeit to a lesser extent. One drawback is that the solution typically is a saddle point, and convergence can be sensitive to how Newton iterations are made when solving the nonlinear problem.
In the limit, the Segregated and the
Fully Coupled solution methods converge to the same solution, but they can have different convergence properties.
In addition to the standard augmented Lagrangian method outlined above, an Augmented Lagrangian, dynamic method is available for transient simulations. As discussed for the penalty method, this formulation is based on the addition of the persistency condition. A segregated solution method is recommended for this method, and the main difference compared to the standard method lies in the definition of the penalized contact pressure. Both the nonpenetration and persistency conditions are enforced by penalizing the rate of the physical gap distance so that
(3-183)
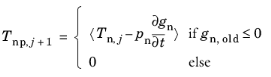
where gn,old is the physical gap distance at the previous increment, and <> is the positive parts operator. The same segregated solution strategy as described above is applied also when the dynamic method is used.
where P is the first Piola-Kirchoff stress,
N is the material normal,
n is the spatial normal, and
Ta is the nominal traction vector. The positive parts operator is used above to indicate that
Tn is strictly positive. The term from
Equation 3-178 in brackets including
δu is also reformulated as
where θ is a parameter used to control the symmetry of the formulation. Using the above definitions,
Equation 3-178 can, after some manipulation and simplification, be rewritten to obtain the weak contribution added by the Nitsche method for normal contact
(3-184)
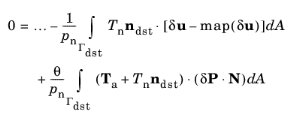
|
•
|
Setting θ = 1 results in a symmetric formulation. The formulation is requires a suitable choice for pn to maintain accuracy and stability. However, it is the most variationally consistent formulation.
|
|
•
|
Setting θ = -1 results in a skew-symmetric formulation. This formulation is less sensitive to the choice of pn.
|
|
•
|
Setting θ = 0 results in a nonsymmetric formulation. This formulation is less sensitive to the choice of pn than the symmetric one, but not as robust as the skew-symmetric. However, this choice causes the term δP to cancel out. For nonlinear materials in particular, this term can be expensive to evaluate, making the nonsymmetric formulation an attractive choice.
|
Note that since the derivation Equation 3-184 started from
Equation 3-178, all of the above choices of
θ will cause a nonsymmetric stiffness matrix when setting of the global system of equations. Also, the penalty factor
pn for the Nitsche’s method can be considered as a stabilization factor, not directly as a spring stiffness as in the penalty method.
The Penalty, dynamic and
Augmented Lagrange, dynamic methods are based on a viscous type formulation, and dissipate energy when the contact is active. The accumulated dissipated energy
Wcntv can be computed by solving a distributed ODE on the destination boundary: