The Plasma Interface

The interface (

), found under the branch (

) couples the Drift Diffusion, Heavy Species Transport, and Electrostatics interfaces into an integrated multiphysics interface to model plasma discharges.

When this physics interface is added, these default nodes are also added to the : , , , and . Then, from the toolbar, add other nodes that implement, for example, boundary conditions and velocity. You can also right-click to select physics features from the context menu.

	Except where described in this section, this physics interface shares it physics nodes with The Drift Diffusion Interface, The Heavy Species Transport Interface, and The Electrostatics Interface.

The is the default physics interface name.

The is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern <name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the name string must be unique. Only letters, numbers, and underscores (_) are permitted in the field. The first character must be a letter.

The default (for the first physics interface in the model) is plas.

Select a — (the default), , or . When using the or models, the mixture averaged diffusion coefficients are automatically computed based on the data specified for each species.

Select the check boxes for which transport mechanisms to — , , , , or . The selection changes the number of Model Inputs requiring values on the page. Note the following:

•

For select that the thermodynamic properties of each reaction and species are computed automatically based on the thermodynamic properties of each species.

•

For it computes a more accurate expression for the Maxwell–Stefan diffusivities. Often the additional correction terms are negligible in which case the expressions are much simpler and the time taken to assemble the Jacobian matrix is reduced.

•

For additional terms are included in the definition of the mass flux vector to ensure that the same solution is obtained regardless of the choice of the species which comes from the mass constraint. This option makes the problem more nonlinear and strongly coupled, and is only necessary when the molecular weights of the species differ substantially (such as a mixture of sulfur hexafluoride and hydrogen).

•

For the tensor form of the ion transport properties when a static magnetic field is present is computed. This option only needs to be activated when a strong DC magnetic field exists and the operating pressure is very low (on the order of millitorr). When this option is activated an expression must be provided for the magnetic flux density, which typically another physics interface computes. This is set in the node.

When the is set to only the properties and are available.

Select the or , or check boxes as needed and select the model for the — (default), , or .

When the is set to only the check boxes and are not available.

Select to compute the tensor form of the electron mobility, electron diffusivity, energy mobility and energy diffusivity. This should only be used in cases where a strong DC magnetic field exists. Two quantities must be supplied, both of which are in the Plasma Model node. The DC mobility which is the value of the electron mobility in the absence of a DC magnetic field and the magnetic flux density which would typically be computed by another physics interface.

Select to specify the electron mobility, diffusivity, energy mobility and energy diffusivity in reduced form. The neutral number density is then specified in the Drift Diffusion Model node. The electron transport properties are computed from the reduced transport properties using:

where Nn is the user-defined neutral number density.

The check box adds an additional term to the definition of the electron current due to gradients in the electron diffusivity. If the diffusivity is a constant then including this does not affect the solution. It is only necessary to include this term if the electron diffusivity is a function of the electron temperature, and there are significant gradients in the electron temperature.

Select (default) to solve the mean electron energy equation self-consistently with the continuity, momentum, and Poisson’s equations, and to use the mean electron energy to parameterize transport and source coefficients. This is the most numerical demanding option to find the mean electron energy because of the strong coupling between the mean electron energy and the electromagnetic fields.

If is selected, it is assumed that transport and source coefficients are well parameterized through the reduced electric field (E/Nn). If or is selected, the computed E/Nn from the fluid plasma equations is used directly as input to the Boltzmann equation in the two–term approximation and the relation between the reduced electric field is automatically computed. If the Boltzmann equation is not solved, the relation between the reduced electric field and the mean electron energy needs to be provided in the section in the node.

When using the local field approximation the fluid equation for the mean electron energy is not solved, which reduces significantly the complexity of the numerical problem. The local field approximation is valid in a situation where the rate of electron energy gain from the electric field is locally balanced by the energy loss rate. When this condition is met the electrons are said to be in local equilibrium with the electric field and the electron mean properties can be expressed as a function of the reduced electric field.

Select to fix the mean electron energy to its initial value. This can be useful in some situations because the strong coupling between the mean electron energy and the electromagnetic fields is removed. This allows for non-self-consistent models to be created quickly, since problems where the mean electron energy is fixed are easier to solve numerically.

This section is available when the is set to . Select a — (the default), , or .

•

solves a closed system where mass and pressure can change, for example, as the result of surface reactions and volume reactions of the associative/dissociative type.

	For more information on the electron energy distribution function (EEDF), see the Theory for the Boltzmann Equation, Two-Term Approximation Interface.

	The options Closed reactor and Constant mass reactor are not supported for stationary studies. If a model uses those options and an attempt is made to use a stationary study an error message appears. Only the Constant pressure option is supported for stationary studies.

If cross section data is used to define source coefficients in the model then an electron energy distribution function (EEDF) needs to be selected. Select one of these options.

where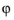

is the mean electron energy (SI unit: eV), ε is the electron energy (SI unit: eV) and Γ is the incomplete gamma function:

•

. Use this option for a generalized distribution function where the EEDF is somewhere between Maxwellian and Druyvesteyn. For this option, specify a power law. This number must be between 1 and 2. Mathematically, the EEDF takes the form:

•

. If a two-dimensional interpolation function has been added to the model, it can be used for the EEDF. In this case, the x-data should be the electron energy (eV) and the y-data should be the mean electron energy (eV).

	The two-dimensional interpolation function can be computed using a parametric sweep in The Boltzmann Equation, Two-Term Approximation Interface. This allows for modeling of discharges where the EEDF is far from Maxwellian. For step-by-step instructions on how to do this, refer to this blog entry: https://www.comsol.com/blogs/the-boltzmann-equation-two-term-approximation-interface/ See Interpolation in the COMSOL Multiphysics Reference Manual.

•

and . Use these options to solve a two-term approximation of the Boltzmann equation.

When or is selected, the EEDF is computed from a partial differential equation instead of taking an assumed function. The following options are available:

•

Select the — (the default), or . This option is only available when is set to and is set to .

•

Select (off by default) if the ionization degree of the discharge is high. The ionization degree and the electron density necessary to model the electron-electron collisions are obtained from the solution of the model equations every time step or iteration. Including this option dramatically increases the computational demand, so it should be avoided if at all possible.

•

Select (on by default) to describe how the energy is split between two electrons when an ionization collision occurs. If selected, then both electrons take an equal energy after the collision. If not selected, the secondary electron created in an ionization collision has zero energy and the ionizing electron carries all the excess energy.

•

Select if the reduced angular frequency of the discharge is high, which is typically only true for microwave discharges. The reduced angular frequency is the ratio of the angular frequency and the neutral number density, ω/N.

•

If the property is active, enter a ω/N (SI unit: m3/s). The default is 10−13 m3/s. If the reduced angular frequency is high, the proportion of electrons with high energies is substantially increased for the same mean electron energy. This is because in DC fields, collisional momentum transfer impedes electrons acquiring higher energies but high frequency fields have the opposite effect.

•

Enter the N (SI unit: dimensionless) to specify the number of mesh elements to use to discretize the underlying energy space. The default is 100, but models with complex gas mixtures may require more.

•

Enter the R (SI unit: dimensionless) to specify the rate at which the mesh coarsens away from the zero energy coordinate. The default is 10, and this does not usually need to be changed. Higher values mean that the mesh will be finer closer to the zero energy, and coarser at higher energies.

•

Select to have the software automatically compute the maximum energy coordinate based on certain assumptions about the EEDF. This is a powerful feature, in that the maximum energy coordinate does not need to be specified, but it does make the problem more nonlinear and thus difficult to solve.

•

Enter the εmax (SI unit: V) to specify the maximum coordinate in energy space on which we are computing the EEDF. When computing the EEDF at high mean energies, this value may need increasing from its default value of 100 V. This option is only available if is not selected.

•

Enter the χε (SI unit: dimensionless) to specify how much the maximum energy coordinate should be scaled. This option is only available if is selected and is set to .

•

Enter the fmin (SI unit: dimensionless) to specify the minimum value that the EEDF should take at the maximum energy coordinate. In order to avoid divide by zero problems, the value should be small and positive. The default value of 1E-15 rarely needs to be changed.

In all these cases the rate constants in the model are automatically computed based on the selected EEDF using the formula:

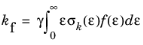The rate coefficients when computed using cross section data are a highly nonlinear function of the mean electron energy. COMSOL Multiphysics automatically computes the integral in Equation 6-1 and makes the result available for evaluation of the rate coefficient. The variation of the rate coefficient for any particular model can be plotted using <name>.kf_<reaction number>. For example, for reaction number 3 in the Plasma interface, with name plas, the rate coefficient is plotted using plas.kf_3.

To display this section, click the button (

) and select in the dialog box.

If the is set to then the solver can run into difficulties as the species mass fractions approach zero. The check box (selected by default) adds an additional source term to the rate expression for each species. In the ι field, enter a tuning parameter for the source stabilization. The default value is 1. This value is usually good enough. If the plasma is high pressure (atmospheric) then it can help to lower this number to somewhere in the range of 0.25–0.5.

The solver can also run into difficulties as the electron density or electron energy density approach zero. The check box (selected by default) adds an additional source term to the equation for the electron density and electron energy density. In the ζ field, enter a tuning parameter for the source stabilization. The default value is 1. This value is usually good enough. If the plasma is high pressure (atmospheric) then it can help to lower this number to somewhere in the range of 0.25–0.5.

To enable this section, click the button (

) and select in the dialog box. This section is only available if one of the following or are used.

It is possible to add and independently. Both check boxes for these methods are selected by default and should remain selected for optimal performance.

Streamline diffusion stabilization is a numerical technique to stabilize the numeric solution of convection-dominated PDEs by adding diffusion in the directions of the streamlines.

To enable this section, click the button (

) and select in the dialog box. This section is only available if one of the following discretizations is used: , , , or .

This method is equivalent to adding a term to the diffusion coefficient in order to dampen the effect of oscillations by making the system somewhat less dominated by convection or migration. If possible, minimize the use of the inconsistent stabilization method because by using it you no longer solve the original problem. By default, the and check boxes are not selected because this type of stabilization adds artificial diffusion and affects the accuracy of the original problem. However, this option can be used to get a good initial guess for underresolved problems.

If required, select the or check boxes and enter a δid,e and/or a δid,i. The default value is 0.25.

Select — , (the default), , , or . The finite element options use the Galerkin method to discretize the equations whereas the option creates degrees of freedom for the dependent variables which are piecewise constant within each mesh element. For the charged species, Scharfetter–Gummel upwinding is used. For charge neutral species and the electrostatic field, a centered difference scheme is used. In cases where the ion and electron flux are strongly driven by the electric field, the option can be more stable. Examples where this is true include dielectric barrier and corona discharges.

The options with log formulation solve for the log of the dependent variables, ensuring that the mass fraction of any of the species is never lower than zero. This makes it more numerically stable but increases the nonlinearity of the equation system, and as such the model might take slightly longer to solve.

When the is set to the sections and are not available.

The dependent variables (field variables) are the , , and . The name can be changed but the names of fields and dependent variables must be unique within a model. The physical meanings of and change depending on the formulation used. For example, when log formulations are used, is the logarithm of the electron density; whereas for other cases, it is the electron density