Multicomponent Diffusion Equations
Suppose a reacting flow consists of k = 1, …, Q species and j = 1, …, N reactions. The equation for the first Q − 1 species is given by
(5-2)
where:
•
jk is the diffusive flux vector
•
Rk is the rate expression for species k (SI unit: kg/(m3·s))
•
u is the mass averaged fluid velocity vector (SI unit: m/s)
•
ρ denotes the density of the mixture (SI unit: kg/m3), and
•
wk is the mass fraction of the kth species (1).
The diffusive flux vector is defined as:
where and Vk is the multicomponent diffusion velocity for species k. The definition of Vk depends on the option chosen for the Diffusion Model property. If Mixture Averaged is chosen then:
(5-3)
where
•
Dk,m is the mixture averaged diffusion coefficient (SI unit: m2/s)
•
Mn is the mean molar mass of the mixture (SI unit: kg/mol)
•
T is the gas temperature (SI unit: K)
•
is the thermal diffusion coefficient for species k (SI unit: kg/(m·s))
•
zk is the charge number for species k (SI unit: dimensionless)
•
μk,m is the mixture averaged mobility for species k (SI unit: m2/(V·s))
•
E is the electric field (SI unit: V/m)
The mixture averaged diffusion coefficient, Dk,m for species k is defined as:
(5-4)
The mean molar mass, Mn is computed using the sum of the mass fractions and molecular weights of all species:
.
The mole fraction for species k, which is required in Equation 5-4 can be computed from the mass fraction of species k and the mean molar mass:
.
The quantity, Dkj is the binary diffusion coefficient between species k and j and are rather complicated functions of the physical properties of the species. They are defined later, in Equation 5-13.
By default, the mixture averaged mobility, μk,m is computed using Einstein’s relation:
where q is the unit charge (SI unit: s A) and kB is Boltzmann’s constant (SI unit: J/K).
If the Mixture diffusion correction is checked, an additional term is added to the right hand side of Equation 5-3
This option makes the problem more non–linear and strongly coupled, and is only necessary when the molecular weights of the species differ substantially (such as a mixture of sulfur hexafluoride and hydrogen).
If the Diffusion Model is changed to Fick’s law then the diffusion coefficient must be given as an input for each species. In this case, the diffusion velocity is defined as:
where Dk,f is the user-defined diffusion coefficient for species k. The mobility for species k is then given by:
.
This approach is much less computationally expensive than the Mixture averaged model since the diffusion coefficients are not computed from the complicated expression in Equation 5-4.
For ions, the mobility can be specified in Mobility Specification through an arbitrary expression, a lookup table as a function of the electric field, or through the Dalgarno or High field mobility models.
When Dalgarno Ref. 8 is selected in the Mobility Specification section the ion mobility is computed as:
where α is the background atom polarizability in Å3, N0 = 2.69·1025 m−3 is the gas number density at 273.15°C and 760 Torr, and mr is the reduced mass
.
Dalgarno’s mobility corresponds to the polarizability limit of the classical Langevin theory Ref. 9. This mobility model gives reasonable values for alkali ions in Ar, Kr, Xe, N2 and H2. This model should not be used in the case resonant charge exchange contributes significantly to the ion transport as it occurs in ions drifting in the parent gas. Moreover, Dalgarno’s mobility is only valid for small electric field strengths that ensure that the ion thermal velocity is much larger than the ion drift velocity. Note that the ion mobility and ion drift velocity are, respectively, independent and directly proportional to the electric field.
When High field is selected in the Mobility Specification section the ion mobility is computed as:
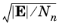
where σ is a cross section characterizing the ion-atom interaction (SI unit: m2). This model is valid when the electric field is high enough to ensures that the ion drift velocity is much larger than the ion thermal velocity Ref. 8. With this model the ion drift velocity is proportional to as is frequently found in experiments in the high field limit.
By default, the mixture averaged diffusivity Dk,m (and Fick’s law diffusivity Dk,f) are computed using Einstein’s relation:
.
There is also the option to use the Local Field Approximation. The local field approximation can be used to compute the ion temperature and thus the diffusivity through Einstein’s relation, see Ref. 7 and Ref. 10. The ion temperature is computed using:
where Mk is the ion mass (SI unit: kg), T is the background gas temperature (SI unit: K), Mn is the mean mass of the mixture (SI unit: kg), and E is the electric field (SI unit: V/m). If the High field mobility model is used the background gas temperature is neglected and the ion temperature is computed as
.