Species Transport Properties

The diffusion coefficients are computed from the following expression based on kinetic gas theory:

(5-13)

Here:

•

Dkj is the binary diffusion coefficient (SI unit: m2/s)

•

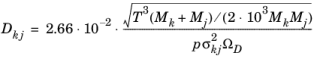
M equals the molecular weight (SI unit: kg/mol)

•

T represents the temperature (SI unit: K)

•

p is the pressure (SI unit: Pa), and

•

σ equals the characteristic length (SI unit: Å) of the Lennard-Jones/Stockmayer potential.

•

In addition, ΩD is the collision integral, given by the following equation (Ref. 2 and Ref. 3):

(5-14)

where

(5-15)

In Equation 5-15, μ is the species dipole moment (SI unit: Debye). For gases at moderate pressure, the binary diffusivity can be used for the multicomponent Maxwell–Stefan diffusivities.

The predefined expression for the dynamic viscosity is given by the kinetic gas theory (Ref. 2 and Ref. 3) as

(5-16)

Here μ represents the dynamic viscosity (SI unit: N·s/m2), and Ωv is the collision integral, given by

with

(5-17)

In Equation 5-17, μ is the species dipole moment (SI unit: Debye). The predefined expression for thermal conductivity comes from the Stiel-Thodos equation (Ref. 4)

(5-18)

where the thermal conductivity k is in (SI unit: W/(m·K)). Here Cp denotes the heat capacity (SI unit: J/(mol·K)).