The Droplet Evaporation feature causes particles to decrease in size over time, by treating them as liquid droplets evaporating in a surrounding gas.

In the physics interface Additional Variables section, you can select one of the following options from the Particle size distribution list: Uniform size, Specify particle diameter, or Specify particle mass.

Because droplet evaporation models involve model particles whose sizes change over the duration of the study, the Droplet Evaporation node can only be added to the model if either Specify particle diameter or Specify particle mass is selected from the Particle size distribution list. If the Uniform size option is selected at any point, than any Droplet Evaporation nodes will be automatically disabled.

Optionally, you can also solve for the particle temperature by selecting the Compute particle temperature check box in the physics interface Additional Variables section. As described in later sections, the evaporation of a droplet can often be treated as a transient heat-up period followed by a period of evaporation at a fixed temperature. If a complete model of both the heat-up and steady-state periods is desired, then the Compute particle temperature check box should be selected and the Stefan-Fuchs evaporation model should be used. This further increases the number of degrees of freedom by one per particle. The initial temperature of the droplets can be set in particle release features such as Inlet and Release from Grid.

The droplet evaporation theory in this section relies on a number of assumptions. For more detailed explanations of many of these assumptions, see Refs. 32 and 33.

After the droplets are first exposed to the gas, the droplet temperature asymptotically approaches a steady-state value known as the wet-bulb temperature. At the wet-bulb temperature, the heat entering the droplet from its surroundings equals the energy lost due to the heat of vaporization. In other words, at the wet-bulb temperature, exactly 100% of the energy entering the droplet is used for phase change, rather than changing the temperature of molecules in the droplet. As will be shown later in the discussion of the Stefan-Fuchs model, the wet-bulb temperature is achieved when the Spalding mass transfer number and Spalding heat transfer number are equal, BM = BT.

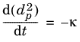
for some constant κ (SI unit: m2/s). This behavior, which has also been shown experimentally, is sometimes called the d2 law, and κ is sometimes called the evaporation constant (Ref. 32, 35, 39, 40). You can enter the value of κ directly by selecting Specify evaporation constant from the Evaporation model list. This approach can give reasonable approximations of the droplet lifetime if the heat-up time is comparatively small. Typical values of κ for mixtures of hydrocarbon fuels with air are on the order of 1 mm2/s (Ref. 35).

The Maxwell model for droplet evaporation is a quasi-steady model of diffusion of vapor from the surface of a liquid sphere. The diffusion equation in the gas surrounding an isolated droplet is (Ref. 36)

Spherical symmetry has been assumed, so that the gradient of the vapor density is only nonzero in the radial (r) direction. Thus Equation 5-22 is only strictly valid when the droplet is perfectly spherical and has zero velocity relative to the surrounding gas.

For r > rp where rp is the particle radius, Equation 5-22 states that the rate of change of the droplet mass is the product of the surface area of a sphere of radius r with the inward mass flux at r. The total mass flow rate across any spherical shell with a radius r > rp must be equal to that of any other spherical shell, or else mass would be accumulating at some radial distance in the gas, violating the steady-state assumption. Therefore dmp/dt is a constant, independent of the radial position r.

In comparing Equation 5-22 to Equation 1.1 in Ref. 36, the former seems to be missing a negative sign. However, Ref. 36 defines the evaporation rate, which would be positive for evaporating droplets; whereas Equation 5-22 defines the time derivative of the particle mass, which would be negative for evaporating droplets.

Rearranging Equation 5-22 yields

where the subscript (a) indicates ambient or free-stream conditions a large distance away from the droplet surface, while the subscript s indicates conditions at the droplet surface. Rearranging this expression gives the so-called Maxwell solution for evaporation of a spherical droplet (Ref. 34),

where R = 8.3144598 J/(mol K) is the universal gas constant, gives the Maxwell evaporation model in terms of the partial vapor pressures at the particle surface and in ambient conditions. The vapor pressure at the surface of the droplet is the saturation vapor pressure because the gas surrounding the particle is assumed to be in thermodynamic equilibrium.

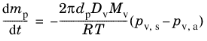
The Stefan-Fuchs evaporation model is an attempt to improve upon the Maxwell model by including the effect of Stefan flow, the bulk motion of the gas-vapor mixture in the region surrounding the droplet.

Assuming also that the diffusion coefficient of the vapor in the gas equals the diffusion coefficient of the gas in the vapor (Dv = Dg), and also that both phases can be treated as ideal gases, the bulk velocity in the radial direction vr (SI unit: m/s) is

Equation 5-22 now has both diffusive and advective components,

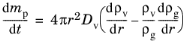
Another simplifying assumption is necessary to solve Equation 5-25. Fuchs (Ref. 36) suggests that the total molar concentration and total pressure are held constant,

whereas Sazhin (Ref. 34) instead suggests that the total mass density should be held constant,

Here, the constant mass density (Ref. 34) will be used,

This last result can be expressed in terms of the dimensionless Spalding mass transfer number BM,

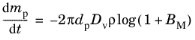
where Mg and Mv (SI unit: kg/mol) are respectively the molar masses of the ambient gas and vapor phases. Thus the mass transfer number can be determined from the saturation vapor pressure at the droplet temperature, the mass fraction or vapor pressure in the gas at large distances from the droplet, and the molar masses of the vapor and the surrounding gas.

If the saturation vapor pressure is very low, which can be true for relatively cool droplets, then ρg,s and ρ are nearly equal, and a first-order Taylor expansion of Equation 5-26 returns the Maxwell solution, Equation 5-23. For example, Fuchs (Ref. 36) observed that for water droplets at 20°C, the inclusion of Stefan flow changes the evaporation rate by about one percent.

The Saturation vapor pressure at droplet surface pv,s can be specified directly or solved for using the Clausius-Claperyon equation. One approximate relation that can be used to define pv,s is

where pv,ref is the saturation vapor pressure at some reference temperature Tref (SI unit: K) and hp (SI unit: J/kg) is the droplet latent heat of vaporization. In some scientific literature, slightly different simplifications of the Clausius–Clapeyron equation are presented, or empirical relations with different fitting parameters may be given (Ref. 32, 34, 35, 36, 38).

An accurate value of the binary diffusion coefficient Dv of the vapor in the surrounding gas is crucial to realistic predictions of droplet lifetimes. In particular, the diffusion coefficient may be highly temperature-dependent.

The Vapor diffusion coefficient may be User defined, or taken From thermal properties. The option From thermal properties includes the assumption that the Lewis number is unity,

where ρt is the total density of the vapor-gas mixture. In other words, the mass diffusivity and thermal diffusivity of the surrounding gas are assumed to be equal. In this case, the evaporation rate (following the Stefan-Fuchs model) becomes (Ref. 35)

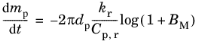
where Cp,r is the specific heat capacity of the vapor-gas mixture, and similarly kr is the thermal conductivity of the mixture. The rule used to compute these mixture-averaged quantities is to weigh the properties of the vapor and gas phases by their mass fractions,

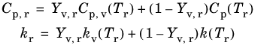
where Yv,r is the reference mass fraction. Here Cp,v(Tr) means that if the specific heat of the vapor is temperature dependent, then it will be evaluated at the reference temperature Tr, and similarly for the other material properties shown.

The reference mass fraction and reference temperature are intended to approximate the material properties in a thin layer surrounding the liquid droplet. They use a weighted average following the one-third rule (Ref. 35, 41),

where Tf is the ambient temperature of the surrounding fluid.

If the Compute particle temperature check box is selected in the physics interface Additional Variables section, then the particle temperature is an additional dependent variable to be solved on each particle, as discussed in the section Computing Particle Temperature. Recall that the square of the droplet diameter tends to decrease at a constant rate after the droplet reaches some equilibrium temperature called the wet-bulb temperature, at which 100% of the energy transferred to the droplet is used to elicit phase change in molecules at the droplet surface, rather than increasing temperature.

If the droplet is colder than the wet-bulb temperature, generally some of the incoming heat is used to raise the droplet temperature. In the Stefan-Fuchs model, this heat source term is (Ref. 35)

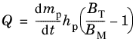
where BT is the dimensionless Spalding heat transfer number,

where the specific heat capacity of the vapor-gas mixture is the average value defined in Equation 5-29.

From Equation 5-30 it is evident that the droplet will heat up if the Spalding heat transfer number is greater than the mass transfer number, or cool down if the Spalding mass transfer number is greater.