Particle Beam Theory

The Particle Beam feature can be used to release nonlaminar particle beams with specified emittance values. The classification of a particle beam as laminar or nonlaminar depends on the distribution of transverse position and velocity within the beam. Further discussion of laminar and nonlaminar beams can be found in Ref. 10.

A beam is laminar if there is a one-to-one relationship between transverse position and velocity. The volume occupied by the beam particles in phase space is essentially zero. In addition, the transverse velocity of particles in a laminar beam must be linearly proportional to the distance from the axis of beam symmetry; otherwise it is possible for particles with unequal transverse velocity components to cross at a later point.

If the beam is nonlaminar, it is possible for the trajectories of particles with different transverse position and velocity components to intersect. Often, such beams occupy nonzero areas in phase space. The area a beam occupies in phase space is related to a quantity known as the emittance that can be defined in several different ways.

The particle beam is released normal to a surface and includes several options for specifying the transverse velocity distribution of beam particles.

If at least one Particle Beam node is present, additional global variables are defined for certain beam properties. Quantities that indicate the distribution of transverse beam position and velocity are defined in a coordinate system that is centered at the average position of beam particles, qav. In 2D, the transverse direction is orthogonal to the average particle velocity vav; in 3D, the two transverse directions are orthogonal to vav and to each other.

Let the transverse displacement from the beam center be denoted x, and the transverse velocity be expressed using the dimensionless variable

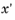
, which is the ratio of transverse velocity to axial velocity. For 3D, the following discussion can be extended to consider two distinct transverse displacement components in orthogonal directions, called for example x1 and x2.

The area of the phase space ellipse is indicated by the beam emittance. In general, beams may exhibit a gradual fall-off in particle number density, so that it is not always possible to define a sharp boundary where the phase space distribution begins and ends. Instead of being treated as the area of a clearly defined geometric entity, the phase space ellipse can be defined in a statistical sense. The 1-rms emittance ε1,rms (SI unit: m) is defined as:

Where the brackets represent an arithmetic mean over all particles. In addition, the 4-rms emittance ε4,rms is frequently reported because it corresponds to the area of an ellipse if the distribution of particles in phase space is uniform:

In addition to the size of the phase space ellipse, several characteristics of its shape can be described using the Twiss parameters α, β, and γ, defined as:

In 3D, it is also possible to define the hyperemittance:

Depending on the way in which the hyperemittance is defined, either the 1-rms or 4-rms emittance may be used.

The Particle Beam node includes built-in options for releasing distributions of particles in velocity space by sampling from uniform or Gaussian distributions in each transverse velocity direction. These distributions can be upright if the initial value of the Twiss parameter α is set to 0. In this case, for the elliptical distributions of particles in phase space, the semimajor and semiminor axes of the ellipse are initially parallel to the x- and

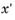
-axes. The initial values of the Twiss parameters must fulfill the Courant–Snyder condition,

Thus, out of the three Twiss parameters, it is only necessary to specify β and α.

Given the initial value of the Twiss parameter β, the 1-rms beam emittance ε and the Twiss parameter α, the initial distribution of particles in phase space depends on the option selected from the list.

The initial particle positions and velocities can be generated by sampling from the following function, as described in Ref. 11:

where a and b are the semi-major and semi-minor axis of the ellipse in physical space,

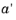
and

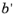
are the envelope angles which are related to the Twiss parameters according to:

The amplitude of A2 can be resolved into two components:

where:

As described in Ref. 11, start by defining two uniformly-distributed random numbers

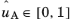
and

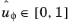
, then define:

with the definition of A depends on the type of distribution and follows later. Now define two additional uniformly-distributed random numbers

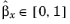
and

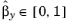
then the relative initial positions are the particles are given by:

and the relative initial transverse velocities by:

The definition of A changes depending on the requested distribution:

Table 4-4: definition of Variable a for different distribution types
KV	Waterbag	parabolic

The Gaussian distribution is generated in a more straightforward way. Let

be normally distributed random numbers with zero mean and standard deviation one. The beam position and velocity can be defined as:

and

Once the relative initial positions and velocities are generated, they are converted to global coordinates using the following:

where rc is the beam centroid, t1 and t2 are the two tangent vectors on the surface, n is the surface normal, and V is the velocity magnitude.

When the is , the same initial values of the Twiss parameter β, Twiss parameter α and beam emittance ε are applied to each of the two transverse directions. When the is , distinct values of these parameters can be assigned to each transverse direction.

When the property is , the is , the is and the is , the is entered instead of the emittance. In this case, the 1−rms emittance is computed from the B (SI unit: A/m2) and the I (SI unit: A) using

When the is set to , the Twiss parameters are computed from the , xm, the , x'm and the , θ using the following

and

The Twiss parameter α is computed by first defining a rotation matrix

then defining the semimajor and semiminor axis using

which results in