
|
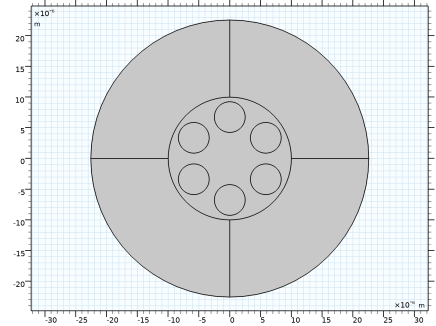
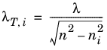 ,
,
|
1
|
|
2
|
In the Select Physics tree, select Optics>Wave Optics>Electromagnetic Waves, Frequency Domain (ewfd).
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file microstructured_optical_fiber_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. Click New.
|
|
6
|
|
7
|
Click OK.
|
|
1
|
|
2
|
Select the object c2 only.
|
|
3
|
|
4
|
|
5
|
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. From the Contribute to list, choose Air Holes.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
In the Typical wavelength text field, type wlr. This parameter approximates the in-plane wavelength.
|
|
1
|
|
2
|
|
3
|
|
4
|
From the Mode search method list, choose Region, as we will search for the complex effective indices in a rectangular region defined by the following parameters.
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Click the
|
|
5
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Global>ewfd.neff - Effective mode index.
|
|
3
|
Click
|
|
1
|
Go to the Table window.
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Scattering Boundary Condition section. From the Scattered wave type list, choose Cylindrical wave.
|
|
5
|
Click to expand the Mode Analysis section. Select the Subtract propagation constant from material wave number check box, to subtract the mode propagation constant from the material wave number when calculating the wave vector component in the radial (normal) direction.
|
|
6
|
|
1
|
|
2
|
|
1
|
Go to the Table window.
|
|
1
|
|
2
|
|
3
|
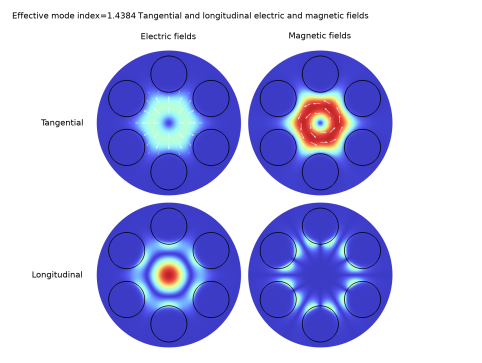
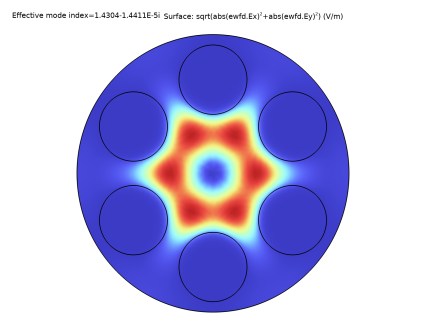
In the Expression text field, type sqrt(abs(ewfd.Ex)^2+abs(ewfd.Ey)^2). This represents the norm of the tangential electric field.
 |
|
1
|
|
2
|
|
3
|
In the Expression text field, type 10*abs(ewfd.Ez). This represents the norm of the longitudinal electric field. This component is scaled by a factor of ten, to make it visible when compared to the tangential electric field components.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd), Ctrl-click to select Surface 1 and Surface 2.
|
|
2
|
Right-click and choose Duplicate.
|
|
1
|
|
2
|
In the Expression text field, type sqrt(abs(ewfd.Hx)^2+abs(ewfd.Hy)^2). This represents the norm of the tangential magnetic field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, expand the Results>Electric Field (ewfd)>Surface 4 node, then click Surface 4.
|
|
2
|
|
3
|
In the Expression text field, type 10*abs(ewfd.Hz). This represents the norm of the longitudinal magnetic field. Again, a scale factor of 10 is used here to make the longitudinal component visible when compared to the tangential components.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Arrow Surface 1 and choose Duplicate.
|
|
2
|
In the Settings window for Arrow Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Electric>ewfd.Ex,ewfd.Ey - Electric field.
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, expand the Results>Datasets node, then click Study 1/Solution 1 (sol1).
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd), Ctrl-click to select Line 1 and Line 2.
|
|
2
|
Right-click and choose Duplicate.
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Results>Electric Field (ewfd)>Line 4 node, then click Translation 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Annotation 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
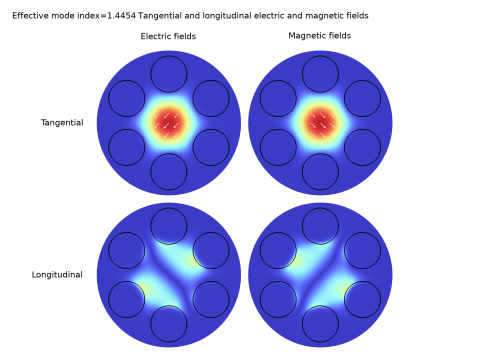
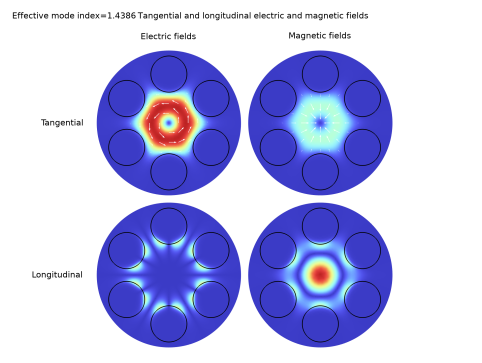
In the Parameter indicator text field, type Effective mode index=eval(ewfd.neff), to update the effective index in the title.
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
13
|