You are viewing the documentation for an older COMSOL version. The latest version is available here.
PDF
Earthquake Analysis of a Building
Introduction
This example shows how to perform an earthquake analysis of a structure using response spectrum analysis.
Earthquakes are, by their nature, not deterministic. If you were to check that a building can sustain an earthquake by time domain analysis, you would have to run a large number of analyses with different representative prescribed acceleration histories for the supports. Such an approach would require large computational resources, and it would still not be guaranteed that the worst possible case is covered.
A response spectrum analysis, on the other hand, requires only an eigenfrequency analysis and possibly the solution of few linear stationary load cases. The severity of the earthquake is represented by a design response spectrum, which is provide by various national and international building codes.
Model Definition
The structure is a regular beam framework. The geometry is parameterized so that it can have any number of columns in both horizontal directions, and any number of floors. Also, the column spacing and floor height are parameters. The geometry used in the analysis is shown in Figure 1.
Figure 1: The geometry of the steel frame.
GEOMETRY
The selected geometrical parameters are:
•
Number of columns in the X direction: 5
•
Column spacing in the X direction: 6 m
•
Number of columns in the Y direction: 4
•
Column spacing in the Y direction: 5 m
•
Number of floors: 4
•
Floor height: 3 m
The following beam cross sections are used:
•
Columns: Box 300-by-200 mm with wall thickness 10 mm. The stiff direction is along the global X-axis.
•
Horizontal beams in the X direction: HEA 260.
•
Horizontal beams in the Y direction: HEA 220.
Material
Structural steel with E = 200 GPa, ν = 0.30, and ρ = 7850 kg/m3.
Mass
The horizontal beams are assigned an additional mass of 1000 kg/m, representing the mass of each floor.
Constraints
The end of all columns are fixed in the ground plane.
Loads
In one study, the deflection under a pure gravitational loading is analyzed.
For the response spectrum evaluations, design response spectra inspired by Eurocode (EN1998-1) are used. The horizontal pseudoacceleration spectrum is shown in Figure 2, and the vertical spectrum is shown in Figure 3. The spectra represent a rather mild earthquake.
Figure 2: Horizontal design response spectrum.
Figure 3: Vertical design response spectrum.
Results and Discussion
Gravity Load
In the first analysis, a pure gravity load is applied to the structure. The stress distribution is shown in Figure 4. The maximal stress occurs at the top of the outermost columns, and it is approximately 60 MPa.
Figure 4: Stress distribution with only gravity load.
Eigenfrequency Analysis
Within the computed range of eigenfrequencies (up to 33 Hz), there are over 500 natural frequencies. The reason for this is the large number of symmetries and near symmetries which such a structure possesses. However, most of the corresponding eigenmodes will not contribute to the earthquake response because they cannot be excited by a homogeneous base movement.
The time for evaluating a result quantity in a response spectrum analysis is proportional to the square of the number of included eigenmodes. For this reason, it is useful to limit the analysis to those eigenmodes that actually contribute significantly to the response.
An investigation of the mass associated with each eigenmode can give an indication of which modes are important. In Figure 5 and Figure 6, the ratio between the modal mass and the total mass is shown for all computed eigenmodes on a linear and logarithmic scale, respectively. It can be seen that over 80% of the mass in both horizontal directions is represented already by the first two modes.
The most important modes for each direction are shown in Figure 7, Figure 8, and Figure 9.
Figure 5: The relative modal mass as function of eigenfrequency.
Figure 6: The relative modal mass as function of eigenfrequency; log scale.
Figure 7: The first eigenmode; bending in the Y direction.
Figure 8: The second eigenmode; bending in the X direction.
Figure 9: The first mode having a significant vertical displacement.
A Combine Solutions node is used to filter the set of computed eigenmodes into a set of modes to be included in the response spectrum analysis. The criterion for inclusion of a mode is
(1)
for at least one direction k. After such filtering, only 23 modes are retained.
First, a standard response spectrum analysis is performed, for which all modes are considered as being fully periodic. The stress and displacement results are shown in Figure 10 and Figure 11, respectively. Note that displacements in a response spectrum analysis are relative to the fixed base which is the ground in this case.
Figure 10: von Mises stress with CQC solution.
Figure 11: Total displacement with CQC solution.
Certain standards require more sophisticated analysis methods. In the next step, two extensions are made:
•
A split is made between periodic and rigid modes, using the Gupta method. Modes with higher natural frequencies are called rigid. The highest frequency at which the modes are fully periodic is set to 10 Hz, and the lowest frequency where the modes are fully in phase with each other is set to 20 Hz.
•
A missing mass correction is used, which provides an additional stationary load containing the mass forces from masses not represented by the eigenmodes. The zero period frequency (the frequency where the acceleration in the response spectrum equals the peak acceleration of the earthquake) is set to 30 Hz.
The stress results from such evaluation are shown in Figure 12. In this case, the deviation from the first evaluation is small; the largest stress is still 151 MPa. The reason is that in this case, the response is dominated by the periodic modes.
Figure 12: von Mises stress after including a missing mass correction.
Application Library path: Structural_Mechanics_Module/Dynamics_and_Vibration/building_response_spectrum
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Structural Mechanics>Beam (beam).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Response Spectrum.
6
Click  Done.
Global Definitions
Geometry Parameters
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, type Geometry Parameters in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file building_response_spectrum_parameters.txt.
Horizontal Spectrum Parameters
1
In the Home toolbar, click  Parameters and choose Add>Parameters.
2
In the Settings window for Parameters, type Horizontal Spectrum Parameters in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file building_response_spectrum_horspec_parameters.txt.
Vertical Spectrum Parameters
1
In the Home toolbar, click  Parameters and choose Add>Parameters.
2
In the Settings window for Parameters, type Vertical Spectrum Parameters in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file building_response_spectrum_vertspec_parameters.txt.
Horizontal Spectrum
1
In the Home toolbar, click  Functions and choose Global>Piecewise.
2
In the Settings window for Piecewise, type Horizontal Spectrum in the Label text field.
3
In the Function name text field, type hsp.
4
Locate the Definition section. In the Argument text field, type T.
5
Find the Intervals subsection. Click  Load from File.
6
Browse to the model’s Application Libraries folder and double-click the file building_response_spectrum_horspec_function.txt.
7
Click  Create Plot.
Results
Horizontal Pseudoacceleration Spectrum
1
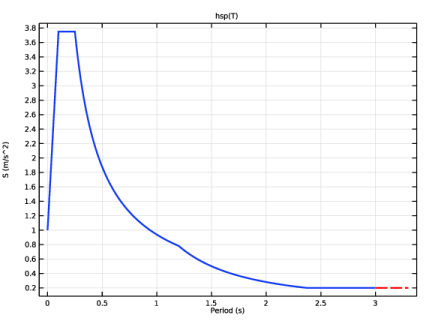
In the Settings window for 1D Plot Group, type Horizontal Pseudoacceleration Spectrum in the Label text field.
2
Locate the Plot Settings section.
3
Select the x-axis label check box. In the associated text field, type Period (s).
4
In the y-axis label text field, type S (m/s^2).
Function 1
1
In the Model Builder window, expand the Horizontal Pseudoacceleration Spectrum node, then click Function 1.
2
In the Settings window for Function, locate the Output section.
3
From the Extrapolation list, choose Right.
4
Click to expand the Coloring and Style section. From the Width list, choose 2.
5
In the Horizontal Pseudoacceleration Spectrum toolbar, click  Plot.
Global Definitions
Vertical Spectrum
1
In the Home toolbar, click  Functions and choose Global>Piecewise.
2
In the Settings window for Piecewise, type Vertical Spectrum in the Label text field.
3
In the Function name text field, type vsp.
4
Locate the Definition section. In the Argument text field, type T.
5
Find the Intervals subsection. Click  Load from File.
6
Browse to the model’s Application Libraries folder and double-click the file building_response_spectrum_vertspec_function.txt.
7
Click  Create Plot.
Results
Vertical Pseudoacceleration Spectrum
1
In the Settings window for 1D Plot Group, type Vertical Pseudoacceleration Spectrum in the Label text field.
2
Locate the Plot Settings section.
3
Select the x-axis label check box. In the associated text field, type Period (s).
4
In the y-axis label text field, type S (m/s^2).
Function 1
1
In the Model Builder window, expand the Vertical Pseudoacceleration Spectrum node, then click Function 1.
2
In the Settings window for Function, locate the Output section.
3
From the Extrapolation list, choose Right.
4
Locate the Coloring and Style section. From the Width list, choose 2.
5
In the Vertical Pseudoacceleration Spectrum toolbar, click  Plot.
Horizontal Pseudoacceleration Spectrum, Vertical Pseudoacceleration Spectrum
1
In the Model Builder window, under Results, Ctrl-click to select Horizontal Pseudoacceleration Spectrum and Vertical Pseudoacceleration Spectrum.
2
Right-click and choose Group.
Design Response Spectra
1
In the Settings window for Group, type Design Response Spectra in the Label text field.
2
In the Model Builder window, collapse the Design Response Spectra node.
Geometry 1
Column
1
In the Geometry toolbar, click  More Primitives and choose Polygon.
2
In the Settings window for Polygon, type Column in the Label text field.
3
Locate the Coordinates section. In the table, enter the following settings:
x (m)
y (m)
z (m)
0
0
0
0
0
WZ
4
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. Click New.
5
In the New Cumulative Selection dialog box, type Columns in the Name text field.
6
Click OK.
Array 1 (arr1)
1
In the Geometry toolbar, click  Transforms and choose Array.
2
Select the object pol1 only.
3
In the Settings window for Array, locate the Size section.
4
In the x size text field, type colX.
5
In the y size text field, type colY.
6
In the z size text field, type nFloors.
7
Locate the Displacement section. In the x text field, type WX.
8
In the y text field, type WY.
9
In the z text field, type WZ.
10
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. From the Contribute to list, choose Columns.
11
Click  Build Selected.
12
Click the  Zoom Extents button in the Graphics toolbar.
Horizontal X direction
1
In the Geometry toolbar, click  More Primitives and choose Polygon.
2
In the Settings window for Polygon, type Horizontal X direction in the Label text field.
3
Locate the Coordinates section. In the table, enter the following settings:
x (m)
y (m)
z (m)
0
0
WZ
WX
0
WZ
4
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. Click New.
5
In the New Cumulative Selection dialog box, type Horizontal X in the Name text field.
6
Click OK.
Array 2 (arr2)
1
In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Array 1 (arr1) and choose Duplicate.
2
In the Settings window for Array, locate the Input section.
3
Find the Input objects subsection. Click to select the  Activate Selection toggle button.
4
From the Input objects list, choose Horizontal X.
5
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. From the Contribute to list, choose Horizontal X.
6
Locate the Size section. In the x size text field, type colX-1.
7
Click  Build Selected.
Horizontal Y direction
1
In the Geometry toolbar, click  More Primitives and choose Polygon.
2
In the Settings window for Polygon, type Horizontal Y direction in the Label text field.
3
Locate the Coordinates section. In the table, enter the following settings:
x (m)
y (m)
z (m)
0
0
WZ
0
WY
WZ
4
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. Click New.
5
In the New Cumulative Selection dialog box, type Horizontal Y in the Name text field.
6
Click OK.
Array 3 (arr3)
1
In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Array 2 (arr2) and choose Duplicate.
2
In the Settings window for Array, locate the Input section.
3
Find the Input objects subsection. Click to select the  Activate Selection toggle button.
4
From the Input objects list, choose Horizontal Y.
5
Locate the Size section. In the x size text field, type colX.
6
In the y size text field, type colY-1.
7
Locate the Selections of Resulting Entities section. Find the Cumulative selection subsection. From the Contribute to list, choose Horizontal Y.
8
Click  Build All Objects.
Foundation
1
In the Geometry toolbar, click  Selections and choose Box Selection.
2
In the Settings window for Box Selection, type Foundation in the Label text field.
3
Locate the Geometric Entity Level section. From the Level list, choose Point.
4
Locate the Box Limits section. In the z maximum text field, type WZ/2.
Beam (beam)
Cross Section Data - Columns
1
In the Model Builder window, under Component 1 (comp1)>Beam (beam) click Cross-Section Data 1.
2
In the Settings window for Cross-Section Data, type Cross Section Data - Columns in the Label text field.
3
Locate the Cross-Section Definition section. From the list, choose Common sections.
4
From the Section type list, choose Box.
5
In the hy text field, type 300[mm].
6
In the hz text field, type 200[mm].
7
In the ty text field, type 10[mm].
8
In the tz text field, type 10[mm].
Section Orientation 1
1
In the Model Builder window, click Section Orientation 1.
2
In the Settings window for Section Orientation, locate the Section Orientation section.
3
From the Orientation method list, choose Orientation vector.
4
Specify the V vector as
1
X
0
Y
0
Z
Cross Section: Horizontal X (HEA260)
1
In the Physics toolbar, click  Edges and choose Cross-Section Data.
2
In the Settings window for Cross-Section Data, type Cross Section: Horizontal X (HEA260) in the Label text field.
3
Locate the Edge Selection section. From the Selection list, choose Horizontal X.
4
Locate the Cross-Section Definition section. From the list, choose Common sections.
5
From the Section type list, choose H-profile.
6
In the hy text field, type 250[mm].
7
In the hz text field, type 260[mm].
8
In the ty text field, type 12.5[mm].
9
In the tz text field, type 7.5[mm].
Section Orientation 1
1
In the Model Builder window, expand the Cross Section: Horizontal X (HEA260) node, then click Section Orientation 1.
2
In the Settings window for Section Orientation, locate the Section Orientation section.
3
From the Orientation method list, choose Orientation vector.
4
Specify the V vector as
0
X
0
Y
1
Z
Cross Section: Horizontal Y (HEA220)
1
In the Model Builder window, right-click Cross Section: Horizontal X (HEA260) and choose Duplicate.
2
In the Settings window for Cross-Section Data, type Cross Section: Horizontal Y (HEA220) in the Label text field.
3
Locate the Edge Selection section. From the Selection list, choose Horizontal Y.
4
Locate the Cross-Section Definition section. In the hy text field, type 210[mm].
5
In the hz text field, type 220[mm].
6
In the ty text field, type 11[mm].
7
In the tz text field, type 7[mm].
Fixed Constraint 1
In the Physics toolbar, click  Points and choose Fixed Constraint.
Added Mass - Horizontal X
1
In the Physics toolbar, click  Edges and choose Added Mass.
2
In the Settings window for Added Mass, type Added Mass - Horizontal X in the Label text field.
3
Locate the Edge Selection section. From the Selection list, choose Horizontal X.
4
Locate the Added Mass section. In the ρL text field, type 1000.
Added Mass - Horizontal Y
1
Right-click Added Mass - Horizontal X and choose Duplicate.
2
In the Settings window for Added Mass, type Added Mass - Horizontal Y in the Label text field.
3
Locate the Edge Selection section. From the Selection list, choose Horizontal Y.
Fixed Constraint 1
1
In the Model Builder window, click Fixed Constraint 1.
2
In the Settings window for Fixed Constraint, locate the Point Selection section.
3
From the Selection list, choose Foundation.
You will start by computing the effects of gravity as a model verification.
Gravity 1
In the Physics toolbar, click  Global and choose Gravity.
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Structural steel.
4
Right-click and choose Add to Component 1 (comp1).
5
In the Home toolbar, click  Add Material to close the Add Material window.
Mesh 1
Edge 1
1
In the Mesh toolbar, click  Boundary and choose Edge.
2
In the Settings window for Edge, locate the Edge Selection section.
3
From the Selection list, choose All edges.
Distribution 1
1
Right-click Edge 1 and choose Distribution.
2
Right-click Distribution 1 and choose Build All.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
Add and run a stationary study to check the gravity load.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Right-click and choose Add Study.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study: Gravity
1
In the Settings window for Study, type Study: Gravity in the Label text field.
2
In the Home toolbar, click  Compute.
Results
Line 1
1
In the Model Builder window, expand the Stress (beam) node, then click Line 1.
2
In the Settings window for Line, locate the Expression section.
3
From the Unit list, choose MPa.
Deformation
1
In the Model Builder window, expand the Line 1 node, then click Deformation.
2
In the Stress (beam) toolbar, click  Plot.
3
In the Home toolbar, click  Add Predefined Plot.
Add Predefined Plot
1
Go to the Add Predefined Plot window.
2
In the tree, select Study: Gravity/Solution 1 (sol1)>Beam>Beam Orientation (beam).
3
Click Add Plot in the window toolbar.
4
In the Home toolbar, click  Add Predefined Plot.
Results
Beam Orientation (beam), Stress (beam)
1
In the Model Builder window, under Results, Ctrl-click to select Stress (beam) and Beam Orientation (beam).
2
Right-click and choose Group.
Gravity Results
1
In the Settings window for Group, type Gravity Results in the Label text field.
2
In the Model Builder window, collapse the Gravity Results node.
Study 1
Step 1: Eigenfrequency
1
In the Model Builder window, under Study 1 click Step 1: Eigenfrequency.
2
In the Settings window for Eigenfrequency, locate the Study Settings section.
3
In the Approximate number of eigenfrequencies text field, type 600.
4
In the Maximum number of eigenfrequencies text field, type 1000.
5
Clear the Perform consistency check check box.
6
In the Model Builder window, click Study 1.
7
In the Settings window for Study, type Study: Eigenfrequency in the Label text field.
Remove Low Mass Modes
1
In the Study toolbar, click  Combine Solutions.
2
In the Settings window for Combine Solutions, type Remove Low Mass Modes in the Label text field.
3
Locate the Combine Solutions Settings section. From the Solution operation list, choose Remove solutions.
4
From the Exclude method list, choose Implicit.
5
In the Excluded if text field, type (comp1.rsp1.mEffLX<comp1.rsp1.mass*massTol)&&(comp1.rsp1.mEffLY<comp1.rsp1.mass*massTol)&&(comp1.rsp1.mEffLZ<comp1.rsp1.mass*massTol).
6
In the Study toolbar, click  Compute.
Once the study is run, set the Combined Solutions node to point to the stored full eigenvalue solution as input. This is necessary in case you want to modify the filtering, and then just rerun the second study step.
7
In the Model Builder window, click Step 2: Remove Low Mass Modes.
8
In the Settings window for Combine Solutions, locate the Combine Solutions Settings section.
9
From the Solution list, choose Study: Eigenfrequency/Solution 2 (sol2).
10
From the Use list, choose Study: Eigenfrequency/Solution Store 1 (sol3).
Results
Examine how the modes contribute to the total mass.
Total Modal Mass
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Total Modal Mass in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Eigenfrequency/Solution 2 (sol2).
4
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Response Spectrum 1>Effective modal mass>rsp1.mEffLX - Effective modal mass, X-translation - kg.
5
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
rsp1.mEffLY
kg
Effective modal mass, Y-translation
rsp1.mEffLZ
kg
Effective modal mass, Z-translation
6
Locate the Data Series Operation section. From the Transformation list, choose Integral.
7
From the Method list, choose Summation.
8
Click  Evaluate.
True Mass
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type True Mass in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study: Eigenfrequency/Solution 2 (sol2).
4
From the Eigenfrequency selection list, choose First.
5
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Definitions>Response Spectrum 1>rsp1.mass - Mass - kg.
6
Click  Evaluate.
Relative Modal Mass Contribution
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Relative Modal Mass Contribution in the Label text field.
3
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
rsp1.mEffLX/rsp1.mass
1
X direction
rsp1.mEffLY/rsp1.mass
1
Y direction
rsp1.mEffLZ/rsp1.mass
1
Z direction
4
Locate the Data section. From the Dataset list, choose Study: Eigenfrequency/Solution Store 1 (sol3).
5
Click  Evaluate.
Table
1
Go to the Table window.
2
Click Table Graph in the window toolbar.
Results
Table Graph 1
1
In the Model Builder window, under Results>1D Plot Group 6 click Table Graph 1.
2
In the Settings window for Table Graph, locate the Coloring and Style section.
3
Find the Line style subsection. From the Line list, choose None.
4
Find the Line markers subsection. From the Marker list, choose Cycle.
5
Click to expand the Legends section. Select the Show legends check box.
Relative Modal Mass
1
In the Model Builder window, under Results click 1D Plot Group 6.
2
In the Settings window for 1D Plot Group, type Relative Modal Mass in the Label text field.
3
Locate the Legend section. From the Position list, choose Middle right.
4
Locate the Plot Settings section.
5
Select the y-axis label check box. In the associated text field, type Relative modal mass.
6
In the Relative Modal Mass toolbar, click  Plot.
7
Click the  y-Axis Log Scale button in the Graphics toolbar.
8
In the Relative Modal Mass toolbar, click  Plot.
Mode Shape (beam)
In the Model Builder window, click Mode Shape (beam).
Arrow Point 1
1
In the Mode Shape (beam) toolbar, click  More Plots and choose Arrow Point.
2
In the Settings window for Arrow Point, click to expand the Inherit Style section.
3
From the Plot list, choose Line 1.
Deformation 1
1
Right-click Arrow Point 1 and choose Deformation.
2
In the Mode Shape (beam) toolbar, click  Plot.
Mode Shape (beam)
1
In the Model Builder window, under Results click Mode Shape (beam).
2
In the Settings window for 3D Plot Group, locate the Data section.
3
From the Eigenfrequency (Hz) list, choose 1.4117.
4
In the Mode Shape (beam) toolbar, click  Plot.
5
From the Eigenfrequency (Hz) list, choose 11.109.
6
In the Mode Shape (beam) toolbar, click  Plot.
Mode Shape (beam), Relative Modal Mass
1
In the Model Builder window, under Results, Ctrl-click to select Mode Shape (beam) and Relative Modal Mass.
2
Right-click and choose Group.
Eigenfrequency Results
1
In the Settings window for Group, type Eigenfrequency Results in the Label text field.
2
In the Model Builder window, collapse the Eigenfrequency Results node.
Add a response spectrum dataset, and enter the evaluation settings.
Response Spectrum 3D 1
1
In the Results toolbar, click  More Datasets and choose Response Spectrum 3D.
2
In the Settings window for Response Spectrum 3D, locate the Data section.
3
From the Eigenfrequency dataset list, choose Study: Eigenfrequency/Solution 2 (sol2).
4
Locate the Spectra section. From the Depends on list, choose Period time.
5
From the Primary horizontal spectrum list, choose Horizontal Spectrum (hsp).
6
From the Secondary horizontal spectrum list, choose Horizontal Spectrum (hsp).
7
From the Vertical spectrum list, choose Vertical Spectrum (vsp).
3D Plot Group 7
In the Results toolbar, click  3D Plot Group.
Line 1
Right-click 3D Plot Group 7 and choose Line.
Stress, CQC Method
1
In the Settings window for 3D Plot Group, type Stress, CQC Method in the Label text field.
2
Locate the Color Legend section. Select the Show maximum and minimum values check box.
Line 1
1
In the Model Builder window, click Line 1.
2
In the Settings window for Line, locate the Expression section.
3
In the Expression text field, type beam.mises.
4
From the Unit list, choose MPa.
5
Locate the Coloring and Style section. From the Line type list, choose Tube.
Stress, CQC Method
1
In the Model Builder window, click Stress, CQC Method.
2
In the Settings window for 3D Plot Group, locate the Data section.
3
From the Dataset list, choose Response Spectrum 3D 1.
4
In the Stress, CQC Method toolbar, click  Plot.
Displacement, CQC Method
1
Right-click Stress, CQC Method and choose Duplicate.
2
In the Settings window for 3D Plot Group, type Displacement, CQC Method in the Label text field.
Line 1
1
In the Model Builder window, expand the Displacement, CQC Method node, then click Line 1.
2
In the Settings window for Line, locate the Expression section.
3
In the Expression text field, type beam.disp.
4
From the Unit list, choose mm.
5
Locate the Coloring and Style section. Click  Change Color Table.
6
In the Color Table dialog box, select Rainbow>Spectrum in the tree.
7
Click OK.
8
In the Displacement, CQC Method toolbar, click  Plot.
Definitions
Investigate the influence of incorporating a correction for the mass not represented by the eigenmodes. In order to do so, you need to set up a particular structure of load cases. This is done from the Response Spectrum node.
Response Spectrum 1 (rsp1)
1
In the Model Builder window, expand the Component 1 (comp1)>Definitions node, then click Response Spectrum 1 (rsp1).
2
In the Settings window for Response Spectrum, click in the upper-right corner of the Response Spectrum section. Locate the Response Spectrum section. Click Create Missing Mass Correction Study in the upper-right corner of the section.
This action added load groups under Global Definitions (Load Groups for Missing Mass Correction), loads in the Beam interface (Loads for Missing Mass Correction), and a new study (Study: Missing Mass Load Cases).
Study: Missing Mass Load Cases
Step 4: Missing Mass Static Load Cases
The gravity load (or any other external loads) should not be part of the missing mass analysis.
1
In the Model Builder window, expand the Study: Missing Mass Load Cases node, then click Step 4: Missing Mass Static Load Cases.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (comp1)>Beam (beam)>Gravity 1.
5
Right-click and choose Disable.
6
In the Home toolbar, click  Compute.
Results
Response Spectrum 3D 2
1
In the Model Builder window, under Results>Datasets right-click Response Spectrum 3D 1 and choose Duplicate.
2
In the Settings window for Response Spectrum 3D, locate the Combination section.
3
From the Rigid modes list, choose Gupta.
4
In the Frequency limit for pure periodic modes text field, type 10.
5
In the Frequency limit for pure rigid modes text field, type 20.
6
In the Zero period acceleration frequency text field, type 30.
7
From the Mass correction list, choose Missing mass method.
8
Locate the Data section. From the Missing mass load cases dataset list, choose Study: Missing Mass Load Cases/Solution 4 (sol4).
Displacement, CQC Method, Stress, CQC Method
1
In the Model Builder window, under Results, Ctrl-click to select Stress, CQC Method and Displacement, CQC Method.
2
Right-click and choose Duplicate.
Stress, CQC Method with Missing Mass Correction
1
In the Settings window for 3D Plot Group, type Stress, CQC Method with Missing Mass Correction in the Label text field.
2
Locate the Data section. From the Dataset list, choose Response Spectrum 3D 2.
3
In the Stress, CQC Method with Missing Mass Correction toolbar, click  Plot.
4
Click  Plot.
Displacement, CQC Method with Missing Mass Correction
1
In the Model Builder window, under Results click Displacement, CQC Method 1.
2
In the Settings window for 3D Plot Group, type Displacement, CQC Method with Missing Mass Correction in the Label text field.
3
Locate the Data section. From the Dataset list, choose Response Spectrum 3D 2.
4
In the Displacement, CQC Method with Missing Mass Correction toolbar, click  Plot.