You are viewing the documentation for an older COMSOL version. The latest version is available here.
PDF
Optimization of an Imported Bracket Geometry — with Parameter Expressions
Introduction
In some application fields, there is a strong focus on weight reduction. For example, this is the case in the automotive industry, where every gram has a distinct price tag.
The bracket in this tutorial is used for mounting a heavy component on a vibrating foundation. It is thus important to keep the natural frequency well above the excitation frequency to avoid resonances. The bracket is also subjected to shock loads, which can be treated as a static acceleration load. This gives an optimization problem, where results from two different study types must be considered simultaneously. In this example, the weight of a mounting bracket is reduced, given an upper bound on the stresses and a lower bound on the first natural frequency, by changing the size and location of three holes on the bracket.
In this tutorial, you will import the bracket geometry from a CAD file and use the Offset Faces and Transform Faces operations as a way to reparameterize the already existing holes in the bracket in order to move and resize them.
An integral part of setting up the optimization is defining the geometrical, or design, constraints, which in this case will make sure that the holes will not come within close proximity of each other or the edges of the bracket. One way you can achieve this is by defining the constraints as parameter expressions based on geometrical relations, and the actual dimensions of the geometry. You can then enter the expressions and their allowed range into the constraint section of the optimization study settings. The solver can then be set to evaluate the design constraints before running the forward problem, and if a constraint expression is out of bounds the solver will continue to the next iteration.
The tutorial Optimization of an Imported Bracket Geometry — with Measuring Dimensions demonstrates an alternative way of setting up geometrical constraints by using measuring dimensions and parameter check features in the geometry sequence to abort the building of the geometry, and the solving of the forward problem for those combinations of the control parameters for which a constraint is outside the allowed range.
Note: This application requires the Optimization Module, the Structural Mechanics Module, and the Design Module.
Model Definition
The original bracket together with a sketched mounted component are shown in Figure 1. The bracket is made of steel.
The component, which can be considered as rigid when compared with the bracket, has its center of gravity at the center of the circular cutout in the bracket. The mass is 4.4 kg, the moment of inertia around its longitudinal axis is 7.1·10−4 kg·m2, and the moment of inertia around the two transverse axes is 9.3·10−4 kg·m2.
Figure 1: Bracket supporting a heavy component.
We can reduce the weight of the bracket by drilling holes in the bracket’s vertical surface and optimizing the holes’ size and placement. This is done by adding the Offset Faces and Transform Faces geometry operations to reparameterize the holes on the imported bracket geometry.
Optimization Parameters
Five geometrical parameters are used in the optimization. They are summarized in Table 1 and shown in Figure 2.
Table 1: Geometrical parameters.
Parameter
Description
Lower limit (mm)
Upper limit (mm)
RC
Radius of the central hole
3
15
ZCO
Vertical distance from the bend to the edge of the central hole
1
23
RO
Radius of the outer hole
3
15
ZOO
Vertical distance from the bend to the edge of the outer hole
8
30
YOO
Horizontal distance from the edge of the bracket to outer hole
3
29
Figure 2: Geometrical parameters that are optimized in the study.
There are two possible paths to take when considering how to set up the control parameters for the optimization. Here we optimize the actual radii and positions of the holes. An alternative would be to define the control parameters that are the displacements relative to the original geometry that is imported from the CAD file.
In the geometry sequence, one Transform Faces node is added to change both the position and the radius, defined by a scaling factor, of the central hole. By using the Transform Faces operation, we can move and change the size of the holes by applying a linear transformation (displacement, rotation, and isotropic scaling) to the faces of the holes. For the outer holes, we add an Offset Faces node to change the radius of the holes and we add two Transform Faces operations to displace the holes. Using the Offset Faces operation, we change the size of the holes on the bracket by offsetting the hole faces in the normal direction.
Constraints
Constraints can be divided into physical constraints and geometrical constraints.
The physical constraints are defined as follows:
•
The lowest natural frequency must be at least 60 Hz.
•
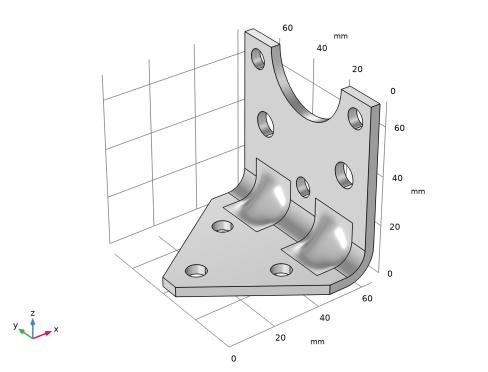
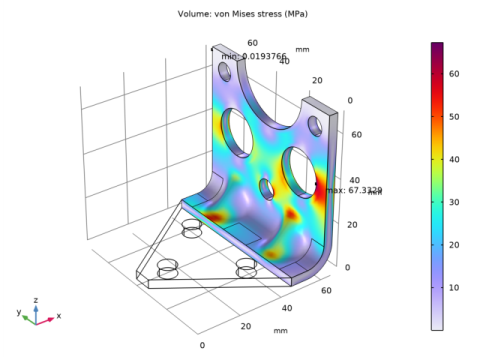
When exposed to a peak acceleration of 4g in all three global directions simultaneously, the effective stress is not allowed to exceed 80 MPa anywhere. This criterion is nondifferentiable because the location of the peak stress can jump from one place to another. A gradient-free optimization algorithm must thus be used.
Geometrical constraints have to ensure that there must be at least 3 mm of material between two holes or between a hole and an edge. This criterion is enforced through limits on the control parameters and as constraints.
The COBYLA solver uses sampling in the control variable space to approximate the objective function, the constraints, and the control variable bounds. Individual samples may be computed outside the bounds and in violation of the constraints. Therefore, it is important to parameterize the geometry in such a way that it is robust with respect to (small) constraints and bound violations.
Bounds and linear constraints are generally satisfied to high precision at the optimum point returned by the solver, but nonlinear constraints are often slightly violated. The reason is that the solver tends to converge from the outside of the feasible domain and terminates before the constraints are completely satisfied. Tightening the solver tolerances will decrease the constraint violation but is often not worth the computational effort; it is better to specify constraints with a safety margin.
Geometrical constraints
The geometrical constraints are shown in Figure 3 and summarized in Table 2.
Figure 3: Geometrical constraints.
As shown in Figure 3, geometrical constraints are set up so that spaces between different geometrical entities are bounded in specific ranges. That is important because we do not want to have very fragile parts of the geometry that would break when loaded, and we want to preserve the original shape of the geometry. Here, we consider four different geometrical constraints, which are summarized in Table 2.
Table 2: Geometrical constraints.
Parameter
Description
Limit (mm)
d_O_Cmp
Distance between the edge of outer hole and component
3
d_O_O
Distance between the edges of two outer holes
3
d_O_C
Distance between the edges of outer and central holes
3
d_C_Cmp
Distance between the edges of central hole and component
3
The geometrical constraints do not depend on the solution of the forward problem and are considered design constraints by the optimization solver. By choosing to strictly enforce design constraints in the optimization study settings, the solver evaluates all design constraints before running the forward problem. If infeasible constraints are found, the forward problem is not run, and the optimization solver proceeds to the next iteration.
Results and Discussion
The initial geometry used in the optimization is shown in Figure 4. Three rather small holes have been introduced.
Figure 4: Initial geometry.
The optimal values of the geometrical parameters are shown in Table 3.
Table 3: Optimal values.
Parameter
Optimal value (mm)
Lower limit (mm)
Upper limit (mm)
RC
5.16
 3
 15
ZCO
4.94
 1
 23
RO
9.66
 3
 15
YOO
4.99
 3
 29
ZOO
16.89
 8
 30
The weight of the optimized bracket is about 189 g, a reduction of 15 g from the original 204.10 g. The stresses from the shock load on the optimized geometry are shown in Figure 5.
Figure 5: Stresses at peak load in the optimized design.
The optimal solution gives three fairly large holes.
There are several possible arrangements of the holes that give the same weight reduction within a small tolerance. It is therefore possible that the design variables are not always the same at convergence.
Notes About the COMSOL Implementation
The bracket geometry is imported from a CAD file saved in STEP format.
The component mounted on the bracket is not modeled in detail. It is replaced by a Rigid Connector having the equivalent inertial properties.
Application Library path: Design_Module/Tutorial_Examples/bracket_import_optimization_expressions
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Structural Mechanics>Solid Mechanics (solid).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Eigenfrequency.
6
Click  Done.
Global Definitions
Parameters 1
The Parameters 1 node contains the parameter expressions used for the model setup. These include the parameters with the original, according to the imported CAD file, dimension values for the features we are optimizing, the parameter expressions used in the offset and transform faces operations that modify the geometry, the parameter expressions for the geometrical constraints, and the parameters used for the physics setup. The expressions in the file you will load into the model have been defined such that the control parameters for the optimization are the actual bolt hole radii and positions (i.e., not the displacement relative to the imported CAD file).
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file bracket_import_optimization_expressions_parameters.txt.
5
In the Home toolbar, click  Parameter Case.
Creating a parameter case for the original design parameters will come in handy when comparing the optimized and unmodified bracket geometry.
6
In the Settings window for Case, type Original Values in the Label text field.
Geometry 1
The bracket geometry for this tutorial has been saved in the STEP format. Make sure that the CAD Import Module geometry kernel is used.
1
In the Model Builder window, under Component 1 click Geometry 1.
2
In the Settings window for Geometry, locate the Advanced section.
3
From the Geometry representation list, choose CAD kernel.
Import 1
1
In the Home toolbar, click  Import.
2
In the Settings window for Import, locate the Import section.
3
Click  Browse.
4
Browse to the model’s Application Libraries folder and double-click the file bracket_import_optimization_geom.step.
5
From the Length unit list, choose From CAD document.
With this option the length unit of the model geometry is automatically set to the unit found in the imported file, in this case, mm. Otherwise, you can manually specify the length unit in the Settings window for the Geometry node.
6
Click  Import.
Coordinate System - Central Hole
Next, set up work planes for the two outer holes and the central hole. These define the coordinate systems that you will use to change the hole size and position using the Transform Faces operation.
1
In the Geometry toolbar, click  Work Plane.
2
In the Settings window for Work Plane, type Coordinate System - Central Hole in the Label text field.
3
Locate the Plane Definition section. From the Plane type list, choose Circle perpendicular.
4
On the object imp1, select Edge 91 only.
5
Click  Build Selected.
Coordinate System - Outer Hole 1
1
In the Geometry toolbar, click  Work Plane.
2
In the Settings window for Work Plane, type Coordinate System - Outer Hole 1 in the Label text field.
3
Locate the Plane Definition section. From the Plane type list, choose Circle perpendicular.
4
On the object imp1, select Edge 99 only.
5
Select the Reverse normal direction check box.
6
Click  Build Selected.
Coordinate System - Outer Hole 2
1
In the Geometry toolbar, click  Work Plane.
2
In the Settings window for Work Plane, type Coordinate System - Outer Hole 2 in the Label text field.
3
Locate the Plane Definition section. From the Plane type list, choose Circle perpendicular.
4
On the object imp1, select Edge 81 only.
5
Click  Build Selected.
Z Displacement and Scaling - Central Hole
For modifying the central hole, you will add the Transform Faces operation to the geometry sequence. Using this feature, you can both displace the hole and change its radius by scaling it.
1
In the Geometry toolbar, click  Editing and choose Transform Faces.
2
In the Settings window for Transform Faces, type Z Displacement and Scaling - Central Hole in the Label text field.
3
On the object imp1, select Boundaries 31 and 32 only.
4
Locate the Coordinate System section. From the Work plane list, choose Coordinate System - Central Hole.
5
Locate the Scaling section. In the Factor text field, type scaleRC.
6
Locate the Displacement section. In the xw text field, type ZCOdisp.
7
Click  Build Selected.
Offset - Outer Holes
For the two outer holes, use the Offset Faces operation to change the radius. Note that only one Offset Faces operation is needed since the holes have the same radius. And two Transform faces operations to displace each hole separately.
1
In the Geometry toolbar, click  Editing and choose Offset Faces.
2
In the Settings window for Offset Faces, type Offset - Outer Holes in the Label text field.
3
On the object tf1, select Boundaries 28, 29, 34, and 35 only.
4
Locate the Offset section. In the Distance text field, type ROoff.
5
Select the Reverse side check box.
6
Click  Build Selected.
Displacement - Outer Hole 1
1
In the Geometry toolbar, click  Editing and choose Transform Faces.
2
In the Settings window for Transform Faces, type Displacement - Outer Hole 1 in the Label text field.
3
On the object off1, select Boundaries 34 and 35 only.
4
Locate the Coordinate System section. From the Work plane list, choose Coordinate System - Outer Hole 1.
5
Locate the Displacement section. In the xw text field, type ZOOdisp.
6
In the zw text field, type YOOdisp.
7
Click  Build Selected.
Displacement - Outer Hole 2
1
In the Geometry toolbar, click  Editing and choose Transform Faces.
2
In the Settings window for Transform Faces, type Displacement - Outer Hole 2 in the Label text field.
3
On the object tf2, select Boundaries 28 and 29 only.
4
Locate the Coordinate System section. From the Work plane list, choose Coordinate System - Outer Hole 2.
5
Locate the Displacement section. In the xw text field, type ZOOdisp.
6
In the zw text field, type YOOdisp.
7
Click  Build Selected.
Work Plane 4
You will define a new work plane that you will use for partitioning the bracket since the evaluation of the maximum stress is needed only for the upper part of the bracket.
1
In the Geometry toolbar, click  Work Plane.
2
In the Settings window for Work Plane, locate the Plane Definition section.
3
From the Plane list, choose yz-plane.
4
From the Offset type list, choose Through vertex.
5
Find the Offset vertex subsection. Click to select the  Activate Selection toggle button.
6
On the object tf3, select Point 18 only.
7
Click  Build Selected.
Partition Objects 1
1
In the Geometry toolbar, click  Booleans and Partitions and choose Partition Objects.
2
Select the object tf3 only.
3
In the Settings window for Partition Objects, locate the Partition Objects section.
4
From the Partition with list, choose Work plane.
5
Click  Build Selected.
At this stage, the geometry set up is ready except for adding a safeguard in case the edges of the central hole and the edges of the faces defining the indentation intersect or come close to each other. This may result in very short edges or narrow face regions, which could become difficult to mesh. Since the indentation edges connect continuous faces, we can use the Ignore Edges virtual operation to hide them from the mesher, and avoid any potential meshing issues. First, create-coordinate based selections that contain the edges for the indentation faces.
Left Edges Indent
1
In the Geometry toolbar, click  Selections and choose Box Selection.
2
In the Settings window for Box Selection, type Left Edges Indent in the Label text field.
3
Locate the Geometric Entity Level section. From the Level list, choose Edge.
4
Locate the Box Limits section. In the x minimum text field, type LX-THK.
5
In the x maximum text field, type LX.
6
In the y minimum text field, type 7[mm].
7
In the y maximum text field, type 22[mm].
8
In the z minimum text field, type 13[mm].
9
In the z maximum text field, type 22[mm].
10
Locate the Resulting Selection section. Find the Cumulative selection subsection. Click New.
11
In the New Cumulative Selection dialog box, type Ignore Edges Selection in the Name text field.
12
Click OK.
13
In the Settings window for Box Selection, click  Build Selected.
Right Edges Indent
1
In the Geometry toolbar, click  Selections and choose Box Selection.
2
In the Settings window for Box Selection, type Right Edges Indent in the Label text field.
3
Locate the Geometric Entity Level section. From the Level list, choose Edge.
4
Locate the Box Limits section. In the x minimum text field, type LX-THK.
5
In the x maximum text field, type LX.
6
In the y minimum text field, type LY-22[mm].
7
In the y maximum text field, type LY-7[mm].
8
In the z minimum text field, type 13[mm].
9
In the z maximum text field, type 22[mm].
10
Locate the Resulting Selection section. Find the Cumulative selection subsection. From the Contribute to list, choose Ignore Edges Selection.
11
Click  Build Selected.
Central Edges Indent
1
In the Geometry toolbar, click  Selections and choose Box Selection.
2
In the Settings window for Box Selection, type Central Edges Indent in the Label text field.
3
Locate the Geometric Entity Level section. From the Level list, choose Edge.
4
Locate the Box Limits section. In the x minimum text field, type LX-2*THK.
5
In the x maximum text field, type LX.
6
In the y minimum text field, type LY/2-8[mm].
7
In the y maximum text field, type LY/2+8[mm].
8
In the z minimum text field, type 0[mm].
9
In the z maximum text field, type 12[mm].
10
Locate the Resulting Selection section. Find the Cumulative selection subsection. From the Contribute to list, choose Ignore Edges Selection.
11
Click  Build Selected.
Ignore Edges 1
1
In the Geometry toolbar, click  Virtual Operations and choose Ignore Edges.
2
In the Settings window for Ignore Edges, locate the Input section.
3
From the Edges to ignore list, choose Ignore Edges Selection.
Change the model view to see the edges on the bottom side of the bracket.
4
Click the  Go to Default View button in the Graphics toolbar.
5
In the Geometry toolbar, click  Build All.
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Structural steel.
4
Click Add to Component in the window toolbar.
5
In the Home toolbar, click  Add Material to close the Add Material window.
Solid Mechanics
Fixed (Bolts)
1
In the Model Builder window, under Component 1 right-click Solid Mechanics and choose Fixed Constraint.
The exact way the bolts clamp the bracket to the foundation is not important for the results in the part being optimized.
2
In the Settings window for Fixed Constraint, type Fixed (Bolts) in the Label text field.
3
Select Boundaries 6–11 only.
Rigid Connector (Mounted component)
1
In the Physics toolbar, click  Boundaries and choose Rigid Connector.
The attached component has a high stiffness, and is bolted to the two upper bolt holes. It is modeled as being rigid, with only mass properties.
2
In the Settings window for Rigid Connector, type Rigid Connector (Mounted component) in the Label text field.
3
Select Boundaries 28, 29, 38, and 39 only.
4
Locate the Center of Rotation section. From the list, choose User defined.
5
Specify the Xc vector as
LX-THK/2
x
LY/2
y
LZ
z
Mass and Moment of Inertia 1
1
In the Physics toolbar, click  Attributes and choose Mass and Moment of Inertia.
2
In the Settings window for Mass and Moment of Inertia, locate the Mass and Moment of Inertia section.
3
In the m text field, type mCmp.
4
From the list, choose Diagonal.
5
In the I table, enter the following settings:
IXCmp
0
0
0
IYZCmp
0
0
0
IYZCmp
Mesh 1
Free Triangular 1
1
In the Mesh toolbar, click  Boundary and choose Free Triangular.
2
Select Boundaries 4, 15, 17, 19, 21, 24, and 26 only.
Size 1
1
Right-click Free Triangular 1 and choose Size.
2
In the Settings window for Size, locate the Geometric Entity Selection section.
3
Click  Clear Selection.
4
Select Boundary 4 only.
5
Locate the Element Size section. From the Predefined list, choose Finer.
Size 2
1
In the Model Builder window, right-click Free Triangular 1 and choose Size.
2
Select Boundaries 15, 17, 19, 21, 24, and 26 only.
3
In the Settings window for Size, locate the Element Size section.
4
From the Predefined list, choose Extra fine.
5
Click  Build Selected.
Swept 1
In the Mesh toolbar, click  Swept.
Distribution 1
1
Right-click Swept 1 and choose Distribution.
2
In the Settings window for Distribution, locate the Distribution section.
3
In the Number of elements text field, type 3.
4
Click  Build All.
Eigenfrequency Study
Run an eigenfrequency study on the initial geometry.
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, type Eigenfrequency Study in the Label text field.
3
In the Home toolbar, click  Compute.
Solid Mechanics
Add the peak loads, and perform a stationary study.
Body load 4g on bracket
1
In the Physics toolbar, click  Domains and choose Body Load.
2
In the Settings window for Body Load, type Body load 4g on bracket in the Label text field.
3
Locate the Domain Selection section. From the Selection list, choose All domains.
4
Locate the Force section. Specify the FV vector as
4*g_const*solid.rho
x
4*g_const*solid.rho
y
4*g_const*solid.rho
z
Rigid Connector (Mounted component)
In the Model Builder window, click Rigid Connector (Mounted component).
Force 4g on mounted component
1
In the Physics toolbar, click  Attributes and choose Applied Force.
2
In the Settings window for Applied Force, type Force 4g on mounted component in the Label text field.
3
Locate the Applied Force section. Specify the F vector as
4*g_const*mCmp
x
4*g_const*mCmp
y
4*g_const*mCmp
z
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Stationary Study
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, type Stationary Study in the Label text field.
3
In the Home toolbar, click  Compute.
Definitions
Prepare for the optimization by adding variables for the bracket mass and the maximum stress.
Stress Optimization Domain
1
In the Definitions toolbar, click  Explicit.
2
In the Settings window for Explicit, type Stress Optimization Domain in the Label text field.
3
Select Domain 2 only.
Domain Probe 1
1
In the Definitions toolbar, click  Probes and choose Domain Probe.
2
In the Settings window for Domain Probe, type mass in the Variable name text field.
3
Locate the Probe Type section. From the Type list, choose Integral.
4
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Solid Mechanics>Material properties>solid.rho - Density - kg/m³.
Domain Probe 2
1
In the Definitions toolbar, click  Probes and choose Domain Probe.
2
In the Settings window for Domain Probe, type maxStress in the Variable name text field.
3
Locate the Probe Type section. From the Type list, choose Maximum.
4
Locate the Source Selection section. From the Selection list, choose Stress Optimization Domain.
5
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Solid Mechanics>Stress>solid.mises - von Mises stress - N/m².
Results
Modify the default stress plot to monitor the geometry and stresses in the optimized region.
Stress in Optimized Region
1
In the Model Builder window, under Results click Stress (solid).
2
In the Settings window for 3D Plot Group, type Stress in Optimized Region in the Label text field.
Volume 1
1
In the Model Builder window, expand the Stress in Optimized Region node, then click Volume 1.
2
In the Settings window for Volume, locate the Expression section.
3
From the Unit list, choose MPa.
Deformation
1
In the Model Builder window, expand the Volume 1 node.
2
Right-click Results>Stress in Optimized Region>Volume 1>Deformation and choose Delete.
Selection 1
1
In the Model Builder window, right-click Volume 1 and choose Selection.
2
In the Settings window for Selection, locate the Selection section.
3
From the Selection list, choose Stress Optimization Domain.
Marker 1
1
Right-click Volume 1 and choose Marker.
2
Click the  Zoom Extents button in the Graphics toolbar.
Root
Set up the optimization study.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Empty Study.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Optimization Study
In the Settings window for Study, type Optimization Study in the Label text field.
Optimization
In the Study toolbar, click  Optimization and choose Optimization.
Eigenfrequency
1
In the Study toolbar, click  Study Reference.
2
In the Settings window for Study Reference, type Eigenfrequency in the Label text field.
3
Locate the Study Reference section. From the Study reference list, choose Eigenfrequency Study.
Stationary
1
In the Study toolbar, click  Study Reference.
2
In the Settings window for Study Reference, type Stationary in the Label text field.
3
Locate the Study Reference section. From the Study reference list, choose Stationary Study.
Optimization
1
In the Model Builder window, click Optimization.
2
In the Settings window for Optimization, locate the Optimization Solver section.
3
From the Method list, choose COBYLA.
4
Find the Solver settings subsection. Clear the Stop if error check box.
5
Locate the Constraints section. Select the Enforce design constraints strictly check box.
6
Click Replace Expression in the upper-right corner of the Objective Function section. From the menu, choose Component 1>Definitions>comp1.mass - Domain Probe 1 - kg.
7
Locate the Objective Function section. In the table, enter the following settings:
Expression
Description
Evaluate for
comp1.mass
Bracket mass
Stationary
The first eigenfrequency is to be used in the optimization.
8
From the Solution list, choose Use first.
9
Locate the Control Variables and Parameters section. Click  Load from File.
10
Browse to the model’s Application Libraries folder and double-click the file bracket_import_optimization_ctrlvars.txt.
11
Locate the Constraints section. In the table, enter the following settings:
Expression
Lower bound
Upper bound
Evaluate for
real(freq)
minFreq
 
Eigenfrequency
comp1.maxStress/maxStressLimit
 
1
Stationary
d_O_Cmp
3[mm]
 
Eigenfrequency
d_C_Cmp
3[mm]
 
Eigenfrequency
d_O_C
3[mm]
 
Eigenfrequency
d_O_O
3[mm]
 
Eigenfrequency
12
Locate the Output While Solving section. Select the Plot check box.
13
From the Plot group list, choose Stress in Optimized Region.
If some configurations are not valid, the optimization procedure should still continue. The default is to stop if an error occurs.
Solution 3
1
In the Study toolbar, click  Show Default Solver.
Run the optimization.
2
Click  Compute.
Results
Stress in Optimized Region
Examine the stress distribution in the optimized configuration.
1
In the Model Builder window, under Results click Stress in Optimized Region.
2
In the Stress in Optimized Region toolbar, click  Plot.
On the last row of Global Constraints Table 7 you will find the values of the natural frequency and maximum stress in the optimized configuration, as well as the values of the other constraints.
Objective Table 3
On the last row of Objective Table 3, you will find the optimal set of parameters and the minimum weight. Note that the value in the Objective column can be colored orange if the solution violates a constraint slightly, but is still accepted within the tolerances.
1
In the Objective Table 3 table, right-click the last row and select Copy Selected Rows to New Parameter Cases.
This last step creates a new parameter case with the optimum parameter values. Next, rebuild the geometry using the optimum parameter values.
Global Definitions
Parameters 1
1
In the Model Builder window, expand the Global Definitions>Parameters 1 node, then click Case 2.
2
In the Settings window for Case, type Optimum values in the Label text field.
3
In the Model Builder window, click Parameters 1.
4
In the Settings window for Parameters, click  Optimum values.
Geometry 1
In the Home toolbar, click  Build All.