PDF
Small Concert Hall Acoustics
Introduction
Designing structures and open spaces with respect to sound quality is important for concert halls, outdoor environments, and even the rooms of a house. Simulating acoustics in the high-frequency limit, where the wavelength is smaller than the geometrical features, is best done with ray acoustics.
This tutorial model shows the basic steps and principles used when setting up a model using the Ray Acoustics physics interface. In the model, the acoustics of a small concert hall is analyzed. The model setup includes an omnidirectional sound source, a directional loudspeaker, wall boundary conditions for specular and diffuse scattering, surface sound pressure level evaluation, analyzing the impulse response, evaluation of objective room acoustic metrics, and a reflectogram. The metric results are compared to simple analytical estimates.
Model Definition
In this model the acoustics of a generic small concert hall is analyzed. Its geometry is depicted in Figure 1. It is a fan-shaped hall with a volume of 460 m3 and a total surface area of 390 m2, fitted with absorbers and diffusers. The location of the different materials is not particularly optimized and does not necessarily follow design rules. Rather than accuracy, the aim of this tutorial is to describe the important modeling steps to perform a room acoustics simulation using ray tracing. The back wall of the room consists of windows and reflective surfaces only, with all the absorption and diffusion being located on the side walls. The stage lies 0.5 m above the ground. The seating area is modeled as a box extruding 1 m high from the ground. It is common practice in ray acoustics to simplify geometry details, and seating is typically represented as a box with equivalent absorption and scattering.
In order to derive the room acoustic metrics, an omnidirectional source is located at the coordinates (xsrc, ysrc, zsrc) at the front of the stage. It generates a pulse that has an SPL of 100 dB at 1 m from the source. The receiver (microphone) is located at the coordinates (xrec, yrec, zrec). These are parameters found under Global Definitions>Parameters. The location of the receiver can be changed in postprocessing, while the location of the source needs to be changed before running the model. The size of the receiver is set to match the common width of a seat, with a receiver radius r = 0.3 m. This value is entered on the Receiver 3D dataset with the Radius input option Fixed size. The number of rays emitted by the source is then determined to limit the error in the calculated impulse response. For an expected error of 1 dB in every time interval Δt of the response, the number of rays should be (see Ref. 1)
(1)
With Δt = 0.01 s, the resulting value gives Nrays = 9000 after rounding up. Determining the number of rays from the volume of the room and the receiver size is a favorable option as default and when there are multiple receivers in the space. Nevertheless, it is also possible to set a desired number of rays and use the predefined expression to calculate the size of the receiver according to the volume of the room, the distance to the source, and the number of rays. This corresponds to the Radius input option Variable size (large room volume) on the Receiver 3D dataset. This option can be an interesting approach in the case of a single receiver. A directional loudspeaker is also included at the coordinates (xspk, yspk, zspk). It is used in a separate study where the sound pressure level in the hall is investigated.
Figure 1: Geometry of the small concert hall.
The absorption properties of the various surfaces (floor, walls, windows, seating, entrance, absorbers, and diffusers) are values taken from Ref. 1–3. The windows are taken as large panes of heavy glass, and the seating area is considered unoccupied. The data is given in octave bands and imported from the file small_concert_hall_absorption_parameters.txt into an interpolation function (lookup table). The scattering coefficients of the diffusers and seating areas are also taken from Ref. 3. For seemingly flat surfaces, a default scattering coefficient s = 0.05 is defined to account for the roughness of the materials. Moreover, the amplitude attenuation of air at 20°C and 50% humidity is imported from the file small_concert_hall_air_attenuation.txt. The imported parameter aair can be entered directly in the Material Properties of Exterior and Unmeshed Domains section, as an amplitude attenuation αext = aair(f0).
Results and Discussion
The first study allows to derive the room impulse response and the objective quality metrics by activating only the omnidirectional source. The local wavefront sound pressure level (SPL) is depicted in Figure 2 after 10 ms and in Figure 3 after 20 ms propagation for the 8 kHz frequency band. This type of plot can be used to inspect holes in the geometry and potential standing wave patterns. Creating an animated version is easily done and can help the visual inspection. When the Compute intensity option is selected in the Ray Acoustics interface, wavefront curvature, intensity, and SPL is calculated along each ray. They allow visualization of the (spatially) local acoustic properties. However, it is the acoustic power transported by each ray that is important when calculating the impulse response (IR) and when visualizing the sound pressure level at surfaces. This means that the Compute power option should always be selected for IR computation, while the Compute intensity can be turned off. Only selecting Compute power will also reduce the number of degrees of freedom (DOFs) solved for, making the model run faster and the size of the saved file smaller. The Count reflections option is also necessary when analyzing the IR.
Figure 2: Ray location and SPL after 10 ms with the omnidirectional source.
Figure 3: Ray location and SPL after 20 ms with the omnidirectional source.
The temporal impulse response (IR) for the source and receiver configuration used in the model is depicted in Figure 4. The frequency domain (FFT) of the IR is depicted in Figure 5. The curve is smoothed with a 1/3-octave running average.
When an IR is reconstructed from a ray tracing simulation, information is inferred and put back into the time signal using the temporal filter kernels. The quality of the simulated IR increases with the number of rays as well as the frequency resolution of the absorption, scattering, and source data (this data can be difficult to get from vendors but can often be simulated). In this model, octave band resolution is used. The Impulse Response plot also allows the use of 1/3-octave and 1/6-octave frequency resolution.
Figure 4: Room impulse response computed at the receiver location.
Figure 5: FFT of the room impulse response (1/3-octave running average).
The IR is further analyzed using the Energy Decay subfeature to the Impulse Response plot. The feature allows the computation of the objective room acoustic metrics like clarity C80; definition D; early decay time EDT; center time ts; reverberation times T20, T30, and T60; and speech transmission index STI. The level decay curves for the seven octave bands used in the model (computed by the Energy Decay subfeature) are depicted in Figure 6. The metrics can be found in the Objective Quality Metrics table in the model (Results>Tables). The values are depicted graphically in Figure 9 and Figure 10.
Figure 6: Level decay curves for the 7 octave bands used in the model.
In order to obtain accurate room acoustic metrics, it is important to ensure the quality of the level decay curves from which they are calculated. The first indicator for quality is the smoothness of the curves. If there are flat sections followed by sudden large drops in level, the number of rays in the simulation should be increased. The default value given in Equation 1 should be sufficient for this in the majority of cases. The second aspect to look at is the amplitude of level decay before the termination point where the curves become vertical and fade out. There should indeed be a large enough decay to fit the definitions of the different room acoustic metrics (for example, T60 takes into account the decay from −5 dB to −65 dB). A general guideline for this to be true is to set the impulse response duration approximately equal to or larger than the reverberation time. This is done in Study 1>Step 1: Ray Tracing>Output times, where the entered values should be 0 and the end time of the simulation. The other parameter controlling the decay amplitude is the energy threshold at which rays are terminated. This threshold should be sufficiently low to avoid losing valuable information. Its value is found in Component 1>Ray Acoustics>Ray Termination 1, where the default recommendation is to use Power as Additional termination criteria and a threshold equal to the initial power of individual rays multiplied by 10−7. This expression ensures a consistent termination criterion according to the source power and number of rays in the simulation, with the factor 10−7 allowing a large enough decay in most cases.
The sound pressure level on the seating area is depicted in Figure 7 for the 8 kHz band. It is calculated using the Sound Pressure Level Calculation feature, available as a subnode to all Wall boundary conditions. In this case it is added to the top surface of the box representing the seating area. The feature can be added to all other walls to postprocess the SPL distribution if necessary.
Figure 7: SPL from the omnidirectional source at the location of the audience.
In the ray tracing method, the intensity I and RMS pressure prms of the nth ray detected by the receiver sphere is expressed as
where Vr is the receiver volume, Lr is the distance traveled by the ray inside the receiver, and Qn is the power carried by the ray (see Ref. 4). The intensity is evaluated using the expression re1dist*rac.Q/re1vol. Plotting this information in a Ray plot as a function of the arrival time yields the (discrete time) energy impulse response, or reflectogram. It is plotted for the 125 Hz and the 8 kHz octave bands in Figure 8. The slope of the curves (point data) gives a visual indication of the reverberation time of the room. In Figure 8 approximate trend lines have been added manually; their slope (from −5 dB to −65 dB which is six decades for log10(In)) gives an estimate of the T60 reverberation time. In this case about 0.5 s for the 8 kHz band and 1 s for the 125 Hz band. These values are seen to fit well with the computed values below.
Figure 8: The raw data of the energetic impulse response or reflectogram. The slope represents the reverberation time in the given octave band.
A comparison between the computed value of reverberation time and simple statistical estimates is shown in Figure 9. To plot the data from the results table the Table Graph plot is used. The estimated values are calculated using the Sabine and Eyring equations used in statistical room acoustics
where V is the room volume, S is the total surface area, aair is the atmospheric amplitude attenuation, and is the average wall absorption (see Ref. 2). The results show a good agreement in this case. However, it is not expected that the Sabine and Eyring predictions always match simulation results closely, especially in rooms where the diffuse sound field assumption does not hold.
Figure 9: Reverberation time estimates based on the Sabine and Eyring formulas compared to the computed reverberation time.
Selected room acoustic metrics are plotted as functions of the octave band center frequency in Figure 10. The definition and clarity metrics are also compared to analytical estimates in the figures. The estimates are based on analytical models of the direct energy, early energy, and late energy (see Ref. 1). They are defined in the Definitions>Variables: Quality Metric Estimates. All metrics should be estimated taking their just noticeable difference (JND) into account when investigating a study case.
Definition D (or D50) gives a metric for syllable intelligibility. In this room it is around 40% to 50% for most bands which is acceptable for a space with a purpose focused on music. The center time ts is another metric that correlates to speech intelligibility, it is not shown here but can be found in the model. The clarity metric C80 is used to characterize the transparency of music, for concert halls typical values lie between −5 dB to +3 dB. In this case the design is not optimal for the higher octave bands.
Several definitions of the reverberation time exist, each using a different decay range to quantify the reverberance of a room, or in other words the rate at which acoustic energy is dissipated. In this case the four variables EDT, T20, T30, and T60 return similar values; this indicates that the room exhibits a rather steady decay over time, a sign that the sound field is close to diffuse conditions.
The speech transmission index STI is a single valued metric for speech intelligibility. It is based on modulation transfer function values (14 frequencies) and seven octave bands. The Modulation transfer function can be plotted using the Energy Decay subfeature. The STI is computed as a single value that combines the information in the seven bands. To get the single metric, change the Band type to Broadband in the Energy Decay plot. Making these changes gives an STI value of 0.61 (this indicates good intelligibility). The STI values plotted as a function of octave band center frequency in Figure 10 are computed based on the apparent signal to noise ratio in each band. When Broadband is selected the values in the different bands contribute with the appropriate weighting.
Figure 10: Objective room acoustic metrics clarity, definition, reverberation times, and speech transmission index plotted as functions of octave band center frequency. The clarity and definition metrics are compared to analytical estimates. The center time can be seen in the step-by-step instructions and in the model.
The second study investigates the sound field resulting from the directional loudspeaker. Its orientation is defined with a rotated coordinate system as depicted in Figure 11. It was set to point towards the audience area in this example. The directivity of the loudspeaker is also shown in Figure 12 with the SPL of the rays at 4 kHz after 5 ms.
Figure 11: Orientation of the directional loudspeaker.
Figure 12: Ray location and SPL after 1 ms with the directional loudspeaker.
The SPL on the top surface of the seats is now considered. As seen in Figure 13, the highest levels are found at the front seats on the side of the loudspeaker and at the back seats thanks to the close wall reflection. A different loudspeaker location or a combination of several loudspeakers should therefore be investigated if the target was to uniformly cover the audience area.
Figure 13: SPL from the directional loudspeaker at the location of the audience.
Notes About the COMSOL Implementation
There are several options that can be selected on the Results node that are useful when working with ray acoustic models and especially when evaluating the impulse response.
•
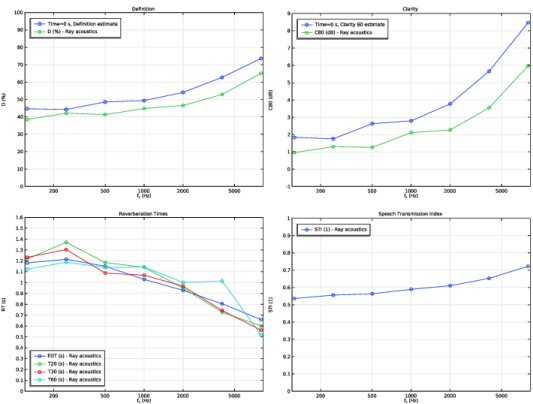
When first setting up plots, it is useful to select the Only plot when requested option as some plots take a long time to render. Another trick is to use only a few rays initially.
•
Once the plots are set up, then before running the model (with a large number of rays), select the Recompute all plot data after solving option. Once the model has solved the plots will be rendered. This is very useful when running the model over lunch break or over night since rendering the IR plot often takes longer time than solving the model.
•
Before saving the model, remember to set the Save plot data list to On. Then all plots do not need to be re-rendered once the model is opened again.
The radiation directivity used in the second study was calculated and imported from a separate loudspeaker model. See the Loudspeaker Driver in a Vented Enclosure model in the Acoustics Module Application Library to learn how to create and export such data.
References
1. M. Vorländer, Auralization, Fundamentals of Acoustics, Modeling, Simulation, Algorithms and Acoustic Virtual Reality, Springer, 2008.
2. H. Kuttruff, Room Acoustics, CRC Press, 2009.
3. T.J. Cox and P. D’Antonio, Acoustic Absorbers and Diffusers: Theory, design and application, Taylor & Francis, 2009.
4. Z. Xiangyang, C. Ke’an, and S. Jincai, “On the accuracy of the ray-tracing algorithms based on various sound receiver models,” Appl. Acoust., vol. 64, pp. 433–441, 2003.
Application Library path: Acoustics_Module/Building_and_Room_Acoustics/small_concert_hall
Modeling Instructions
This section contains the modeling instructions for the Small Concert Hall model. They are followed by the Geometry Modeling Instructions section.
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Acoustics>Geometrical Acoustics>Ray Acoustics (rac).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Ray Tracing.
6
Click  Done.
Geometry 1
The geometry is set up by importing a geometry sequence. The sequence imports the small concert hall geometry and sets up several selections. The predefined selections simplify the rest of the model setup.
1
In the Geometry toolbar, click Insert Sequence and choose Insert Sequence.
2
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_geom_sequence.mph.
3
In the Geometry toolbar, click  Build All.
4
Click the  Wireframe Rendering button in the Graphics toolbar.
5
Click the  Zoom Extents button in the Graphics toolbar.
Import the model parameters from the files. The parameters include the band center frequency f0, the location of the source and receiver, as well as the room volume.
Global Definitions
Parameters 1 - Model
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, type Parameters 1 - Model in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_parameters_model.txt.
Parameters 2 - Source and Receiver Positions
1
In the Home toolbar, click  Parameters and choose Add>Parameters.
2
In the Settings window for Parameters, type Parameters 2 - Source and Receiver Positions in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_parameters_source_positions.txt.
Parameters 3 - Source and Receiver Settings
1
In the Home toolbar, click  Parameters and choose Add>Parameters.
2
In the Settings window for Parameters, type Parameters 3 - Source and Receiver Settings in the Label text field.
3
Locate the Parameters section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_parameters_source_settings.txt.
Create an interpolation function to import the loudspeaker directivity data.
Interpolation 1 (int1)
1
In the Home toolbar, click  Functions and choose Global>Interpolation.
2
In the Settings window for Interpolation, locate the Definition section.
3
From the Data source list, choose File.
4
Click  Browse.
5
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_radiation_balloon.txt.
6
In the Number of arguments text field, type 3.
7
Click  Import.
8
Find the Functions subsection. In the table, enter the following settings:
Function name
Position in file
preal
1
pimag
2
9
Locate the Units section. In the Function table, enter the following settings:
Function
Unit
preal
Pa
pimag
Pa
10
In the Argument table, enter the following settings:
Argument
Unit
Column 1
Hz
Column 2
rad
Column 3
rad
Proceed and set up interpolation functions for the absorption coefficients of the different surfaces in the concert hall. The data is easily stored in one .txt file. Also define an interpolation function for the amplitude attenuation of air (given at 50% relative humidity and 20°C).
Interpolation 2 (int2)
1
In the Home toolbar, click  Functions and choose Global>Interpolation.
2
In the Settings window for Interpolation, locate the Definition section.
3
From the Data source list, choose File.
4
Click  Browse.
5
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_absorption_parameters.txt.
6
In the Number of arguments text field, type 1.
7
Click  Import.
8
Find the Functions subsection. In the table, enter the following settings:
Function name
Position in file
a_walls
1
a_entrance
2
a_windows
3
a_floor
4
a_diffuser
5
a_seats
6
a_absorbers
7
9
Locate the Interpolation and Extrapolation section. From the Interpolation list, choose Nearest neighbor.
10
Locate the Units section. In the Function table, enter the following settings:
Function
Unit
a_walls
1
a_entrance
1
a_windows
1
a_floor
1
a_diffuser
1
a_seats
1
a_absorbers
1
11
In the Argument table, enter the following settings:
Argument
Unit
Column 1
Hz
Interpolation 3 (int3)
1
In the Home toolbar, click  Functions and choose Global>Interpolation.
2
In the Settings window for Interpolation, locate the Definition section.
3
From the Data source list, choose File.
4
Click  Browse.
5
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_air_attenuation.txt.
6
Click  Import.
7
In the Function name text field, type a_air.
8
Locate the Interpolation and Extrapolation section. From the Interpolation list, choose Nearest neighbor.
9
Locate the Units section. In the Argument table, enter the following settings:
Argument
Unit
t
Hz
10
In the Function table, enter the following settings:
Function
Unit
a_air
1/m
Now create the rotated coordinate system that will represent the orientation of the directional loudspeaker. When working on your own model, it is recommended to run a quick study to visualize the coordinate system and ensure that the correct angles are entered.
Definitions
Rotated System 2 (sys2)
1
In the Definitions toolbar, click  Coordinate Systems and choose Rotated System.
2
In the Settings window for Rotated System, locate the Rotation section.
3
Find the Euler angles (Z-X-Z) subsection. In the α text field, type alpha0.
4
In the β text field, type beta0.
5
In the γ text field, type gamma0.
Add a point to the geometry to represent the loudspeaker position. This will allow to later plot the rotated coordinate system.
Geometry 1
Point 1 (pt1)
1
In the Geometry toolbar, click  More Primitives and choose Point.
2
In the Settings window for Point, locate the Point section.
3
In the x text field, type x_spk.
4
In the y text field, type y_spk.
5
In the z text field, type z_spk.
6
In the Geometry toolbar, click  Build All.
Import the variables that define the room acoustic quality metric estimates. They include the reverberation time (T60), based on the Sabine and Eyring estimation equations, clarity (C80), definition (D), and center time (ts). This also requires setting up integration operators for all the surfaces.
Definitions
Integration 1 (intop1)
1
In the Model Builder window, expand the Component 1 (comp1)>Definitions node.
2
Right-click Definitions and choose Nonlocal Couplings>Integration.
3
In the Settings window for Integration, type intop_windows in the Operator name text field.
4
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
5
From the Selection list, choose Windows.
Integration 2 (intop2)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_seats in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Seats.
Integration 3 (intop3)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_diffusers in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Diffusers.
Integration 4 (intop4)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_floor in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Floor.
Integration 5 (intop5)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_entrance in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Entrance.
Integration 6 (intop6)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_walls in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Walls.
Integration 7 (intop7)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_absorbers in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
From the Selection list, choose Absorbers.
Variables: Quality Metric Estimates
1
Right-click Definitions and choose Variables.
2
In the Settings window for Variables, type Variables: Quality Metric Estimates in the Label text field.
3
Locate the Variables section. Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_variables.txt.
Proceed to set up and define the physics and boundary conditions of the model. To compute the impulse response, it is necessary to model the power along the rays and count the reflections. In the model the intensity is also computed along the rays. The intensity represents spatially local properties of the acoustic field approximated by the rays. The model only uses a surface mesh. Propagation in the unmeshed domains requires the definition of material properties at the interface level (in the section Material Properties of Exterior and Unmeshed Domains). Set up boundary conditions for the different walls. All the boundary conditions are defined as Mixed diffuse and specular reflection, with either a default or specific scattering coefficient.
Ray Acoustics (rac)
1
In the Model Builder window, under Component 1 (comp1) click Ray Acoustics (rac).
2
In the Settings window for Ray Acoustics, locate the Intensity Computation section.
3
From the Intensity computation list, choose Compute intensity and power.
4
Locate the Material Properties of Exterior and Unmeshed Domains section. In the cext text field, type c0.
5
In the ρext text field, type rho0.
6
In the αext text field, type a_air(f0).
7
Locate the Additional Variables section. Select the Count reflections check box.
Ray Properties 1
1
In the Model Builder window, under Component 1 (comp1)>Ray Acoustics (rac) click Ray Properties 1.
2
In the Settings window for Ray Properties, locate the Ray Properties section.
3
In the f text field, type f0.
Wall: Walls
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Walls in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Walls.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_default.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_walls(f0).
7
In the αd text field, type a_walls(f0).
Wall: Entrance
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Entrance in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Entrance.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_default.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_entrance(f0).
7
In the αd text field, type a_entrance(f0).
Wall: Windows
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Windows in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Windows.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_default.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_windows(f0).
7
In the αd text field, type a_windows(f0).
Wall: Floor
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Floor in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Floor.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_default.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_floor(f0).
7
In the αd text field, type a_floor(f0).
Wall: Diffusers
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Diffusers in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Diffusers.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_diffuser.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_diffuser(f0).
7
In the αd text field, type a_diffuser(f0).
In this model the scattering coefficient s_diffuser is constant across the frequency bands. It can of course also be defined as an interpolation function that depends on f0.
Wall: Absorbers
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Absorbers in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Absorbers.
4
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
5
In the γs text field, type 1-s_default.
6
Locate the Reflection Coefficients Model section. In the αs text field, type a_absorbers(f0).
7
In the αd text field, type a_absorbers(f0).
Wall: Seats (Top)
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Seats (Top) in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Manual.
4
Select Boundary 41 only.
5
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
6
In the γs text field, type 1-s_seats.
7
Locate the Reflection Coefficients Model section. In the αs text field, type a_seats(f0).
8
In the αd text field, type a_seats(f0).
Sound Pressure Level Calculation 1
1
In the Physics toolbar, click  Attributes and choose Sound Pressure Level Calculation.
2
In the Settings window for Sound Pressure Level Calculation, locate the Smoothing section.
3
Select the Compute smoothed accumulated variable check box.
Wall: Seats (Around)
1
In the Physics toolbar, click  Boundaries and choose Wall.
2
In the Settings window for Wall, type Wall: Seats (Around) in the Label text field.
3
Locate the Boundary Selection section. From the Selection list, choose Manual.
4
Select Boundaries 39, 40, 42, and 59 only.
5
Locate the Wall Condition section. From the Wall condition list, choose Mixed diffuse and specular reflection.
6
In the γs text field, type 1-s_seats.
7
Locate the Reflection Coefficients Model section. In the αs text field, type a_seats(f0).
8
In the αd text field, type a_seats(f0).
The source is defined here with its spatial directivity, reference level, and reference distance. For spatial directivity, the default value shows the angle variables in the cosine and sine expressions needed to define the directivity. In this case, it is set to 0[dB] to obtain an omnidirectional point source.
Source with Directivity 1
1
In the Physics toolbar, click  Global and choose Source with Directivity.
2
In the Settings window for Source with Directivity, locate the Initial Position section.
3
Specify the q0 vector as
x_src
x
y_src
y
z_src
z
4
Locate the Ray Direction Vector section. In the Nw text field, type Nrays.
5
Locate the Intensity and Power section. In the D(φθ,) text field, type 0[dB].
6
In the Lref text field, type L0_src.
7
In the Rref text field, type R0_src.
A second source is included in the model to demonstrate the case of a directional loudspeaker source. In this case, the radiation data is given as the sound pressure measured one meter away from the source; it therefore needs to be converted to sound pressure level.
Source with Directivity 2
1
In the Physics toolbar, click  Global and choose Source with Directivity.
2
In the Settings window for Source with Directivity, locate the Coordinate System Selection section.
3
From the Coordinate system list, choose Rotated System 2 (sys2).
4
Locate the Initial Position section. Specify the q0 vector as
x_spk
x
y_spk
y
z_spk
z
5
Locate the Ray Direction Vector section. In the Nw text field, type Nrays.
6
Locate the Intensity and Power section. In the D(φθ,) text field, type 20*log10(abs(preal(f0,rac.swd2.phi,rac.swd2.theta)+i*pimag(f0,rac.swd2.phi,rac.swd2.theta))/sqrt(2)/20e-6[Pa]).
7
In the Lref text field, type L0_spk.
8
In the Rref text field, type R0_spk.
Ray Termination 1
1
In the Physics toolbar, click  Global and choose Ray Termination.
Add a termination condition to end the propagation of rays once their energy drops below a certain threshold. This allows for faster computations by removing rays which do not have a significant contribution anymore. The if statement and isdefined operator allow to select the correct variable according to the active source.
2
In the Settings window for Ray Termination, locate the Termination Criteria section.
3
From the Spatial extents of ray propagation list, choose Bounding box, from geometry.
4
From the Additional termination criteria list, choose Power.
5
In the Qth text field, type if(isdefined(rac.swd1.Q0),rac.swd1.Q0*1e-7,rac.swd2.Q0*1e-7).
Now create the mesh. In ray tracing simulations for room acoustics, the mesh is used to detect the collisions between rays and boundaries. Therefore, only the boundaries need to be meshed and the element size can be set to a coarse value without compromising accuracy.
Mesh 1
1
In the Model Builder window, under Component 1 (comp1) click Mesh 1.
2
In the Settings window for Mesh, locate the Sequence Type section.
3
From the list, choose User-controlled mesh.
Size
1
In the Model Builder window, under Component 1 (comp1)>Mesh 1 click Size.
2
In the Settings window for Size, locate the Element Size section.
3
From the Predefined list, choose Extra coarse.
Free Triangular 1
1
In the Model Builder window, click Free Triangular 1.
2
In the Settings window for Free Triangular, locate the Boundary Selection section.
3
From the Selection list, choose All boundaries.
Size 1
1
Right-click Free Triangular 1 and choose Size.
Add a finer mesh on the surface where the SPL is computed.
2
In the Settings window for Size, locate the Geometric Entity Selection section.
3
Click  Clear Selection.
4
Select Boundary 41 only.
5
Locate the Element Size section. Click the Custom button.
6
Locate the Element Size Parameters section.
7
Select the Maximum element size check box. In the associated text field, type 0.3.
Mesh the vertices that are not part of the model boundaries.
Vertex 1
1
In the Mesh toolbar, click  Boundary and choose Vertex.
2
In the Settings window for Vertex, locate the Point Selection section.
3
Click  Paste Selection.
4
In the Paste Selection dialog box, type 11 in the Selection text field.
5
Click OK.
6
In the Settings window for Vertex, click  Build All.
Proceed and solve the model with the omnidirectional source by adding a parametric sweep over the center frequency variable f0. This represents the center frequency of the octave bands analyzed in this model, in order to get a broadband response. The first time you set up and solve the model it can be useful to reduce the number of rays by changing the value of the parameter Nrays to, for example, 1000. This will make solving and postprocessing faster. Remember that the quality of the results in acoustic ray tracing increase for an increasing number of rays and more narrow frequency bands (you need to have wall absorption data with the desired resolution). In the Ray Acoustics interface the impulse response plot can handle octave, 1/3-octave, and 1/6-octave data.
Study 1 - Omnidirectional Source
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, type Study 1 - Omnidirectional Source in the Label text field.
Step 1: Ray Tracing
1
In the Model Builder window, under Study 1 - Omnidirectional Source click Step 1: Ray Tracing.
2
In the Settings window for Ray Tracing, locate the Study Settings section.
3
From the Time unit list, choose s.
4
In the Output times text field, type 0 1.6.
For optimal performance only enter 0 and the end time for the simulation. In postprocessing, when reconstructing the impulse response, additional exact time steps for all the wall reflections are used and rendered.
5
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
6
In the tree, select Component 1 (comp1)>Ray Acoustics (rac)>Source with Directivity 2.
7
Click  Disable.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
Using the parametric sweep is important as this gives the frequency resolution (here in full octaves). The ray propagation model is solved once per frequency band. The data is collected in postprocessing, by the receiver dataset and the impulse response plot, to generate the broadband impulse response.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
In the table, click to select the cell at row number 1 and column number 2.
5
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
f0 (Band center frequency)
 
Hz
6
Click  Range.
7
In the Range dialog box, choose ISO preferred frequencies from the Entry method list.
8
In the Start frequency text field, type 125.
9
In the Stop frequency text field, type 8000.
10
Click Replace.
Solving the model takes a couple of minutes and uses less than 4 GB of RAM (depending on your hardware). This will increase for an increasing number of rays.
11
In the Study toolbar, click  Compute.
Results
Ray Trajectories (rac)
1
In the Settings window for 3D Plot Group, locate the Data section.
2
From the Time (s) list, choose Interpolation.
3
In the Time text field, type 10[ms].
4
In the Ray Trajectories (rac) toolbar, click  Plot.
Ray Trajectories 1
1
In the Model Builder window, expand the Ray Trajectories (rac) node, then click Ray Trajectories 1.
2
In the Settings window for Ray Trajectories, locate the Coloring and Style section.
3
Find the Line style subsection. From the Type list, choose None.
4
Find the Point style subsection. From the Type list, choose Point.
Color Expression 1
1
In the Model Builder window, expand the Ray Trajectories 1 node, then click Color Expression 1.
2
In the Settings window for Color Expression, locate the Expression section.
3
In the Expression text field, type rac.Lp.
4
In the Ray Trajectories (rac) toolbar, click  Plot.
This should reproduce the image in Figure 2.
Ray Trajectories (rac)
1
In the Model Builder window, under Results click Ray Trajectories (rac).
2
In the Settings window for 3D Plot Group, locate the Data section.
3
In the Time text field, type 20[ms].
4
In the Ray Trajectories (rac) toolbar, click  Plot.
This should reproduce the image in Figure 3.
Create an animation to visualize early reflections and wave patterns.
Animation 1
1
In the Results toolbar, click  Animation and choose Player.
2
In the Settings window for Animation, locate the Animation Editing section.
3
From the Time selection list, choose Interpolated.
4
Click  Range.
5
In the Range dialog box, type 3[ms] in the Start text field.
6
In the Step text field, type 1[ms].
7
In the Stop text field, type 50[ms].
8
Click Replace.
9
In the Settings window for Animation, locate the Frames section.
10
In the Number of frames text field, type 48.
11
Click the  Play button in the Graphics toolbar.
On the Results node you have several options that are useful when postprocessing ray tracing simulations, where rendering plots can be time consuming. This is especially true for the impulse response plots. While setting up plots, it is useful to select Only plot when requested such that the plots are not generated every time you change an option. It is also good practice to save the plots in the model such that they are already rendered when you open your model at a later stage. Finally, once you have set up all the plots and you are ready to run the model again, it can be useful to enable Recompute all plot data after solving. All plots will then be recomputed after the model is solved, for example, running over lunch.
12
In the Model Builder window, click Results.
13
In the Settings window for Results, locate the Update of Results section.
14
Select the Only plot when requested check box.
15
Select the Recompute all plot data after solving check box.
16
Locate the Save Data in the Model section. From the Save plot data list, choose On.
Also turn on the Plot Information Section to display rendering time and other useful information. This option applies to the whole COMSOL installation; if selected, the Plot Information Section will also appear in other models opened at a later stage.
17
Click the  Show More Options button in the Model Builder toolbar.
18
In the Show More Options dialog box, select Results>Plot Information Section in the tree.
19
In the tree, select the check box for the node Results>Plot Information Section.
20
Click OK.
Now set up the Receiver dataset used for creating the impulse response and subsequent analysis.
Receiver 3D - All Bands
1
In the Model Builder window, expand the Results>Datasets node.
2
Right-click Results>Datasets and choose More 3D Datasets>Receiver 3D.
3
In the Settings window for Receiver 3D, type Receiver 3D - All Bands in the Label text field.
4
Locate the Receiver section. Find the Center subsection. In the x text field, type x_rec.
5
In the y text field, type y_rec.
6
In the z text field, type z_rec.
7
Find the Radius subsection. From the Radius input list, choose Fixed size.
8
In the Radius text field, type r_rec.
The default recommendation is to use a receiver radius of 0.3 m, which corresponds to the standard width of a seat. For different applications, especially smaller spaces like a car cabin, it is recommended to decrease the value of the receiver radius.
Receiver 3D - 125 Hz Band
1
In the Model Builder window, right-click Receiver 3D - All Bands and choose Duplicate.
2
In the Settings window for Receiver 3D, type Receiver 3D - 125 Hz Band in the Label text field.
3
Locate the Data section. From the Parameter selection (f0) list, choose From list.
4
In the Parameter values (f0 (Hz)) list, select 125.
Receiver 3D - 8 kHz Band
1
In the Model Builder window, right-click Receiver 3D - 125 Hz Band and choose Duplicate.
2
In the Settings window for Receiver 3D, type Receiver 3D - 8 kHz Band in the Label text field.
3
Locate the Data section. From the Parameter selection (f0) list, choose From list.
4
In the Parameter values (f0 (Hz)) list, select 8000.
Impulse Response
1
In the Results toolbar, click  1D Plot Group.
2
In the Settings window for 1D Plot Group, type Impulse Response in the Label text field.
3
Locate the Data section. From the Dataset list, choose Receiver 3D - All Bands.
Impulse Response 1
1
In the Impulse Response toolbar, click  More Plots and choose Impulse Response.
To get sharper filters you can modify some settings in the Advanced section.
2
In the Settings window for Impulse Response, click to expand the Advanced section.
3
In the Np text field, type 22050.
4
In the δ text field, type 0.001.
Rendering the impulse response will typically take one or two minutes (depending on hardware, number of rays, and frequency band resolution). Once the plot has been generated (the first time) the necessary ray data is cached and any subsequent changes/updates of the plot is faster. The rendering time for the last time a figure was plotted can be found in the first subnode of its plot group, under Information in the Settings window.
5
In the Impulse Response toolbar, click  Plot.
This should reproduce the impulse response shown in Figure 4. The impulse response is the most important result of this model. The signal can be exported under the Export node and used for further analysis in an external signal processing tool. The response is reconstructed from the ray data detected by the Receiver dataset (arrival time, power, and band center frequency). It has a default sampling frequency of 44100 Hz. This can also be changed under the Advanced section in the plot settings window.
Plot 1
1
Right-click Impulse Response 1 and choose Add Plot Data to Export.
2
In the Settings window for Plot, locate the Output section.
3
From the File type list, choose WAVE audio file (*.wav).
4
In the Filename text field, type small_concert_hall_impulse_response.wav.
5
Click to expand the Advanced section. From the Encoding list, choose 16-bit.
Click Export to produce a wav file with the impulse response. This file could be used for auralization or analysis with other tools. Remember to disable any Energy Decay subfeature before exporting.
Proceed to analyze the impulse response with the Energy Decay subfeature. This will create a plot of the level/energy decay and a table with the objective quality metrics.
Energy Decay 1
1
In the Model Builder window, expand the Results>Impulse Response node.
2
Right-click Impulse Response 1 and choose Energy Decay.
3
In the Settings window for Energy Decay, locate the Display section.
4
From the Band type list, choose Individual bands.
5
From the Band frequency list, choose All frequencies.
6
From the Plot list, choose Level decay.
7
Locate the Table section. Find the Early energy subsection. Clear the C50 , Clarity check box.
8
Clear the tr , First ray arrival time check box.
9
Find the Speech intelligibility subsection. Clear the SNR, Apparent SNR check box.
10
Click the  Show Legends button in the Graphics toolbar.
11
In the Impulse Response toolbar, click  Plot.
This should reproduce the image in Figure 6.
To show the impulse response signal again, simply disable the Energy Decay subfeature and click Plot again.
For the sake of this tutorial, the impulse response is generated again and an FFT of the transient signal is performed (duplicate the plot and disable the Energy Decay subfeature). Since a new plot is now generated, the IR data has to be computed again. Creating the plot based on the existing IR plot would have been faster as the data is cached.
Impulse Response 1
1
In the Model Builder window, right-click Impulse Response and choose Duplicate.
2
Expand the Impulse Response 1 node.
Energy Decay 1
1
In the Model Builder window, expand the Results>Impulse Response 1>Impulse Response 1 node.
2
Right-click Energy Decay 1 and choose Disable.
Impulse Response FFT
1
In the Model Builder window, under Results click Impulse Response 1.
2
In the Settings window for 1D Plot Group, type Impulse Response FFT in the Label text field.
3
Locate the Axis section. Select the x-axis log scale check box.
4
Locate the Legend section. Clear the Show legends check box.
When performing an FFT, the energy contained in the time signal is split between positive and negative frequencies. The Show > Frequency spectrum option with Scale > Multiply by sampling period applies the correct scaling factors to obtain physically meaningful results in dB for positive frequencies.
Impulse Response 1
1
In the Model Builder window, expand the Impulse Response FFT node, then click Impulse Response 1.
2
In the Settings window for Impulse Response, locate the x-Axis Data section.
3
From the Transformation list, choose Discrete Fourier transform.
4
From the Show list, choose Frequency spectrum.
5
From the Scale list, choose Multiply by sampling period.
6
Select the Frequency range check box.
7
In the Minimum text field, type 100.
8
In the Maximum text field, type 10000.
9
Select the In dB check box.
10
From the dB type list, choose 20log.
11
From the dB reference list, choose Manual.
12
In the Reference value text field, type rac.pref_SPL.
13
In the Impulse Response FFT toolbar, click  Plot.
This is the raw transfer function of the room (no smoothing).
14
In the Model Builder window, click Impulse Response 1.
15
Locate the Smoothing section. Select the Moving average check box.
16
From the Type list, choose 1/n octave.
17
In the n text field, type 3.
18
In the Impulse Response FFT toolbar, click  Plot.
This should reproduce the image in Figure 5.
Seats SPL
1
In the Home toolbar, click  Add Plot Group and choose 3D Plot Group.
2
In the Settings window for 3D Plot Group, type Seats SPL in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Omnidirectional Source/Parametric Solutions 1 (sol2).
4
Locate the Color Legend section. Select the Show units check box.
Surface 1
1
Right-click Seats SPL and choose Surface.
2
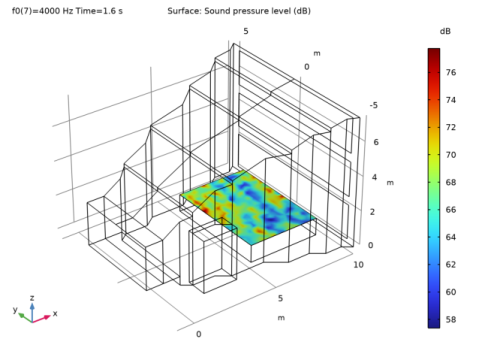
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Ray Acoustics>Accumulated variables>Wall intensity comp1.rac.wall8.spl1.Iw>rac.wall8.spl1.Lp - Sound pressure level - dB.
3
Locate the Expression section. From the Unit list, choose dB.
4
In the Seats SPL toolbar, click  Plot.
This should reproduce the image in Figure 7. The 8 kHz band is chosen per default. A smoothed variable for the SPL also exists rac.wall8.spl1.Lp_sm.
Reflectogram
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Reflectogram in the Label text field.
3
Click to expand the Title section. From the Title type list, choose Label.
4
Locate the Plot Settings section.
5
Select the x-axis label check box. In the associated text field, type t (s).
6
Select the y-axis label check box. In the associated text field, type log10(Power).
7
Locate the Data section. From the Dataset list, choose None.
8
Locate the Axis section. Select the y-axis log scale check box.
Ray 1
1
In the Reflectogram toolbar, click  More Plots and choose Ray.
2
In the Settings window for Ray, locate the Data section.
3
From the Dataset list, choose Receiver 3D - 125 Hz Band.
4
Locate the y-Axis Data section. In the Expression text field, type re1dist*rac.Q/re1vol.
5
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
6
Find the Line markers subsection. From the Marker list, choose Point.
7
Click to expand the Legends section. From the Legends list, choose Manual.
8
Select the Show legends check box.
9
In the table, enter the following settings:
Legends
f<sub>c</sub> = 125 Hz
Ray 2
1
Right-click Ray 1 and choose Duplicate.
2
In the Settings window for Ray, locate the Data section.
3
From the Dataset list, choose Receiver 3D - 8 kHz Band.
4
Locate the Legends section. In the table, enter the following settings:
Legends
f<sub>c</sub> = 8000 Hz
5
In the Reflectogram toolbar, click  Plot.
This should reproduce the image in Figure 8.
T60 - Estimates and Model
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type T60 - Estimates and Model in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Omnidirectional Source/Parametric Solutions 1 (sol2).
4
From the Time selection list, choose First.
5
Click to expand the Title section. From the Title type list, choose Label.
6
Locate the Plot Settings section.
7
Select the x-axis label check box. In the associated text field, type f<sub>c</sub> (Hz).
8
Locate the Axis section. Select the Manual axis limits check box.
9
In the x minimum text field, type 120.
10
In the x maximum text field, type 8322.
11
In the y minimum text field, type 0.
12
In the y maximum text field, type 1.6.
13
Select the x-axis log scale check box.
14
Locate the Legend section. From the Position list, choose Lower left.
Global 1
1
Right-click T60 - Estimates and Model and choose Global.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
T60_S
s
Reverberation time (Sabine)
T60_Sna
s
Reverberation time (Sabine, no air absorption)
T60_E
s
Reverberation time (Eyring)
4
Locate the x-Axis Data section. From the Axis source data list, choose f0.
5
Click to expand the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Star.
Table Graph 1
1
In the Model Builder window, right-click T60 - Estimates and Model and choose Table Graph.
2
In the Settings window for Table Graph, locate the Data section.
3
From the x-axis data list, choose fc (Hz).
4
From the Plot columns list, choose Manual.
5
In the Columns list, select T60 (s).
6
Locate the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Circle.
7
Click to expand the Legends section. Select the Show legends check box.
8
Find the Prefix and suffix subsection. In the Suffix text field, type - Ray acoustics.
9
In the T60 - Estimates and Model toolbar, click  Plot.
This should reproduce the image in Figure 9.
Definition
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Definition in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Omnidirectional Source/Parametric Solutions 1 (sol2).
4
From the Time selection list, choose First.
5
Click to expand the Title section. From the Title type list, choose Label.
6
Locate the Plot Settings section.
7
Select the x-axis label check box. In the associated text field, type f<sub>c</sub> (Hz).
8
Select the y-axis label check box. In the associated text field, type D (%).
9
Locate the Axis section. Select the Manual axis limits check box.
10
In the x minimum text field, type 120.
11
In the x maximum text field, type 8322.
12
In the y minimum text field, type 0.
13
In the y maximum text field, type 100.
14
Select the x-axis log scale check box.
15
Locate the Legend section. From the Position list, choose Upper left.
Global 1
1
Right-click Definition and choose Global.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
D
s
Definition estimate
4
Locate the x-Axis Data section. From the Axis source data list, choose f0.
5
Click to expand the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Star.
Table Graph 1
1
In the Model Builder window, right-click Definition and choose Table Graph.
2
In the Settings window for Table Graph, locate the Data section.
3
From the x-axis data list, choose fc (Hz).
4
From the Plot columns list, choose Manual.
5
In the Columns list, select D (%).
6
Locate the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Circle.
7
Click to expand the Legends section. Select the Show legends check box.
8
Find the Prefix and suffix subsection. In the Suffix text field, type - Ray acoustics.
9
In the Definition toolbar, click  Plot.
This should reproduce the first image in Figure 10.
Clarity
1
Right-click Definition and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Clarity in the Label text field.
3
Locate the Plot Settings section. In the y-axis label text field, type C80 (dB).
4
Locate the Axis section. In the x minimum text field, type 120.
5
In the x maximum text field, type 8322.
6
In the y minimum text field, type -1.
7
In the y maximum text field, type 9.
Global 1
1
In the Model Builder window, expand the Clarity node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
C80
 
Clarity 80 estimate
Table Graph 1
1
In the Model Builder window, click Table Graph 1.
2
In the Settings window for Table Graph, locate the Data section.
3
In the Columns list, select C80 (dB).
4
In the Clarity toolbar, click  Plot.
This should reproduce the second image in Figure 10.
Center Time
1
In the Model Builder window, right-click Clarity and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Center Time in the Label text field.
3
Locate the Plot Settings section. In the y-axis label text field, type ts (s).
4
Locate the Axis section. In the x minimum text field, type 120.
5
In the x maximum text field, type 8322.
6
In the y minimum text field, type 0.
7
In the y maximum text field, type 0.2.
8
Locate the Legend section. From the Position list, choose Lower left.
Global 1
1
In the Model Builder window, expand the Center Time node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
ts
 
Center time estimate
Table Graph 1
1
In the Model Builder window, click Table Graph 1.
2
In the Settings window for Table Graph, locate the Data section.
3
In the Columns list, select ts (s).
4
In the Center Time toolbar, click  Plot.
Reverberation Times
1
In the Model Builder window, right-click Center Time and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Reverberation Times in the Label text field.
3
Locate the Plot Settings section. In the y-axis label text field, type RT (s).
4
Locate the Axis section. In the x minimum text field, type 120.
5
In the x maximum text field, type 8322.
6
In the y minimum text field, type 0.
7
In the y maximum text field, type 1.6.
Global 1
1
In the Model Builder window, expand the Reverberation Times node.
2
Right-click Results>Reverberation Times>Global 1 and choose Delete.
Table Graph 1
1
In the Model Builder window, under Results>Reverberation Times click Table Graph 1.
2
In the Settings window for Table Graph, locate the Data section.
3
In the Columns list, choose EDT (s), T20 (s), T30 (s), and T60 (s).
4
In the Reverberation Times toolbar, click  Plot.
This should reproduce the third image in Figure 10.
Speech Transmission Index
1
In the Model Builder window, right-click Reverberation Times and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Speech Transmission Index in the Label text field.
3
Locate the Plot Settings section. In the y-axis label text field, type STI (1).
4
Locate the Axis section. In the x minimum text field, type 120.
5
In the x maximum text field, type 8322.
6
In the y minimum text field, type 0.
7
In the y maximum text field, type 1.
8
Locate the Legend section. From the Position list, choose Upper left.
Table Graph 1
1
In the Model Builder window, expand the Speech Transmission Index node, then click Table Graph 1.
2
In the Settings window for Table Graph, locate the Data section.
3
In the Columns list, select STI (1).
4
In the Speech Transmission Index toolbar, click  Plot.
This should reproduce the fourth image in Figure 10.
Center Time, Clarity, Definition, Reverberation Times, Speech Transmission Index
1
In the Model Builder window, under Results, Ctrl-click to select Definition, Clarity, Center Time, Reverberation Times, and Speech Transmission Index.
2
Right-click and choose Group.
Objective Quality Metric Plots
In the Settings window for Group, type Objective Quality Metric Plots in the Label text field.
Next, solve the model with the directional loudspeaker using a parametric sweep that fits the frequency range of the speaker data. The criterion value for ray termination should also be updated to match the source variable.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Ray Tracing.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2 - Directional Loudspeaker
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, type Study 2 - Directional Loudspeaker in the Label text field.
Step 1: Ray Tracing
1
In the Model Builder window, under Study 2 - Directional Loudspeaker click Step 1: Ray Tracing.
2
In the Settings window for Ray Tracing, locate the Study Settings section.
3
From the Time unit list, choose s.
4
In the Output times text field, type 0 1.6.
5
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
6
In the tree, select Component 1 (comp1)>Ray Acoustics (rac)>Source with Directivity 1.
7
Click  Disable.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
In the table, click to select the cell at row number 1 and column number 2.
5
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
f0 (Band center frequency)
 
Hz
6
Click  Range.
7
In the Range dialog box, choose ISO preferred frequencies from the Entry method list.
8
In the Start frequency text field, type 63.
9
In the Stop frequency text field, type 4000.
10
Click Replace.
11
In the Study toolbar, click  Compute.
Results
Ray Trajectories (rac) 1
1
In the Settings window for 3D Plot Group, locate the Data section.
2
From the Time (s) list, choose Interpolation.
3
In the Time text field, type 1[ms].
Ray Trajectories 1
1
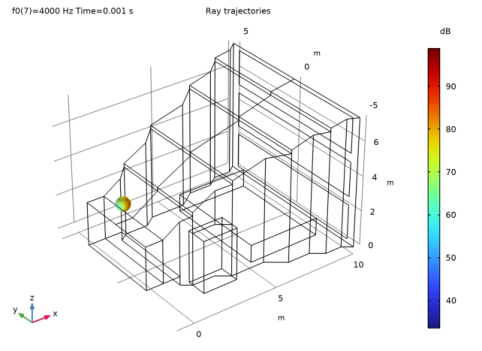
In the Model Builder window, expand the Ray Trajectories (rac) 1 node, then click Ray Trajectories 1.
2
In the Settings window for Ray Trajectories, locate the Coloring and Style section.
3
Find the Line style subsection. From the Type list, choose None.
4
Find the Point style subsection. From the Type list, choose Point.
Color Expression 1
1
In the Model Builder window, expand the Ray Trajectories 1 node, then click Color Expression 1.
2
In the Settings window for Color Expression, locate the Expression section.
3
In the Expression text field, type rac.Lp.
4
In the Ray Trajectories (rac) 1 toolbar, click  Plot.
This should reproduce the image in Figure 12.
Loudspeaker Orientation
1
In the Home toolbar, click  Add Plot Group and choose 3D Plot Group.
2
In the Settings window for 3D Plot Group, type Loudspeaker Orientation in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 2 - Directional Loudspeaker/Solution 10 (sol10).
4
Click to expand the Selection section. From the Geometric entity level list, choose Point.
5
Select Point 11 only.
Coordinate System Point 1
1
Right-click Loudspeaker Orientation and choose More Plots>Coordinate System Point.
2
In the Settings window for Coordinate System Point, locate the Coordinate System section.
3
From the Coordinate system list, choose Rotated System 2 (sys2).
4
Locate the Coloring and Style section.
5
Select the Scale factor check box. In the associated text field, type 2.
6
In the Loudspeaker Orientation toolbar, click  Plot.
This should reproduce the image in Figure 11.
Seats SPL 1
1
In the Model Builder window, right-click Seats SPL and choose Duplicate.
2
In the Settings window for 3D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 2 - Directional Loudspeaker/Parametric Solutions 2 (sol11).
4
In the Seats SPL 1 toolbar, click  Plot.
This should reproduce the image in Figure 13.
Geometry Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Blank Model.
Add Component
In the Home toolbar, click  Add Component and choose 3D.
Geometry 1
Import 1 (imp1)
1
In the Home toolbar, click  Import.
2
In the Settings window for Import, locate the Import section.
3
Click  Browse.
4
Browse to the model’s Application Libraries folder and double-click the file small_concert_hall.mphbin.
5
Click  Import.
6
Click the  Wireframe Rendering button in the Graphics toolbar.
Delete Entities 1 (del1)
1
In the Model Builder window, right-click Geometry 1 and choose Delete Entities.
2
On the object imp1, select Boundary 40 only.
Extrude 1 (ext1)
1
In the Geometry toolbar, click  Extrude.
2
On the object del1, select Boundary 39 only.
3
In the Settings window for Extrude, locate the Distances section.
4
Select the Reverse direction check box.
5
Click  Build Selected.
Delete Entities 2 (del2)
1
Right-click Geometry 1 and choose Delete Entities.
2
On the object ext1, select Boundary 41 only.
Windows
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Windows in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 63–65 only.
Seats
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Seats in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 39–42 and 59 only.
Diffusers
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Diffusers in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 13, 15, 29, 30, 43, 44, 51, and 52 only.
Floor
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Floor in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 3, 8, 12, 14, 18, and 21 only.
Entrance
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Entrance in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 16, 19, 20, 23, 31, and 32 only.
Walls
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Walls in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 1, 2, 4–7, 9–11, 17, 22, 24–28, 34–37, 45–50, 53–58, and 60–62 only.
Absorbers
1
In the Geometry toolbar, click  Selections and choose Explicit Selection.
2
In the Settings window for Explicit Selection, type Absorbers in the Label text field.
3
Locate the Entities to Select section. From the Geometric entity level list, choose Boundary.
4
On the object del2, select Boundaries 33 and 38 only.
Form Union (fin)
1
In the Model Builder window, click Form Union (fin).
2
In the Settings window for Form Union/Assembly, click  Build Selected.