
|
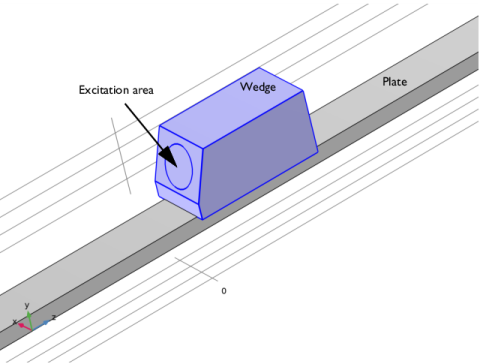
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file lamb_waves_ndt_plate_geometry_parameters.txt.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file lamb_waves_ndt_plate_model_parameters.txt.
|
|
5
|
|
1
|
In the Model Builder window, under Global Definitions right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
Locate the Material Properties section. In the Material properties tree, select Basic Properties>Density.
|
|
4
|
|
5
|
|
6
|
Locate the Material Properties section. In the Material properties tree, select Solid Mechanics>Linear Elastic Material>Pressure-Wave and Shear-Wave Speeds.
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
Locate the Material Properties section. In the Material properties tree, select Basic Properties>Density.
|
|
4
|
|
5
|
|
6
|
Locate the Material Properties section. In the Material properties tree, select Solid Mechanics>Linear Elastic Material>Pressure-Wave and Shear-Wave Speeds.
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose More Materials>Material Link.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Linear Elastic Material 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Mode Analysis.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
Click
|
|
5
|
|
1
|
|
2
|
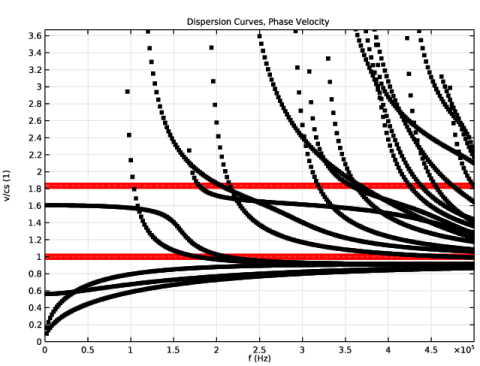
In the Settings window for 1D Plot Group, type Dispersion Curves, Phase Velocity in the Label text field.
|
|
3
|
Locate the Data section. From the Dataset list, choose Study 1 - Mode Analysis/Parametric Solutions 1 (sol2).
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
13
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
|
|
9
|
|
10
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
Locate the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
In the Logical expression for inclusion text field, type (abs(imag(solid.kn))<1)&&(real(solid.kn)>0).
|
|
4
|
|
1
|
|
2
|
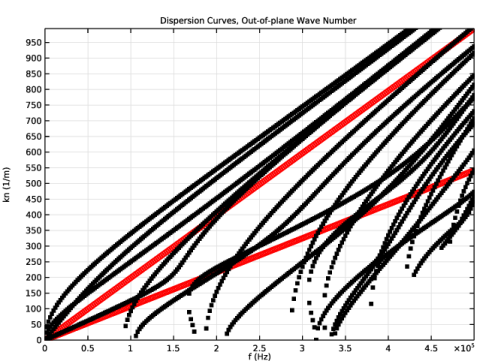
In the Settings window for 1D Plot Group, type Dispersion Curves, Out-of-plane Wave Number in the Label text field.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the Dispersion Curves, Out-of-plane Wave Number node, then click Global 1.
|
|
2
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
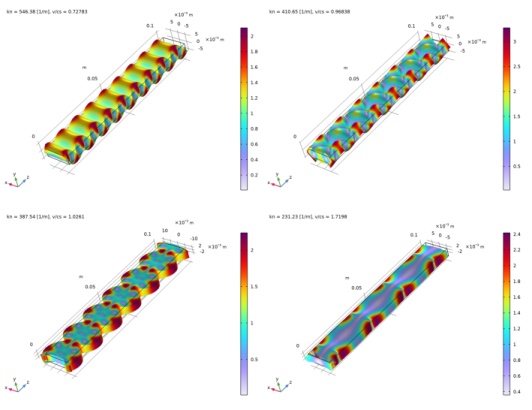
In the Parameter indicator text field, type kn = eval(real(solid.kn)) [1/m], v/cs = eval(omega0/real(solid.kn)/cs_steel).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file lamb_waves_ndt_plate_geom_sequence.mph.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Definition section. In the Expression text field, type sin(omega0*t)*(1 - cos(omega0*t/4))*rect1(t).
|
|
5
|
|
6
|
|
8
|
|
9
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 2 (comp2) right-click Materials and choose More Materials>Material Link.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1 - Mode Analysis.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 2 (comp2)>Definitions, Ctrl-click to select Point Probe 1 (point1), Point Probe 2 (point2), Point Probe 3 (point3), and Point Probe 4 (point4).
|
|
2
|
Right-click and choose Group.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
Locate the Element Size Parameters section. In the Maximum element size text field, type v_lamb/(1.5*2*f0).
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for Free Tetrahedral, click to expand the Element Quality Optimization section.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Solid Mechanics (solid).
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Values of Dependent Variables section. Find the Store fields in output subsection. From the Settings list, choose For selections.
|
|
5
|
|
6
|
|
7
|
Click OK.
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
In the Model Builder window, expand the Probe Plot Displacements node, then click Probe Table Graph 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Locate the Data section. From the Dataset list, choose Study 2 - Wave Propagation/Solution 253 (4) (sol253).
|
|
4
|
|
5
|
|
6
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
5
|
Locate the Legends section. In the table, enter the following settings:
|
|
6
|
|
1
|
|
2
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file lamb_waves_ndt_plate_geometry_parameters.txt.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
Select the object ext1 only.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, right-click Geometry 1 and choose Booleans and Partitions>Partition Objects.
|
|
2
|
Select the object blk1 only.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
On the object par1, select Domain 2 only.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
On the object fin, select Boundary 31 only.
|
|
3
|