Error estimation is available in the Adaptation and Error Estimation section of the Stationary, Eigenfrequency, and Frequency Domain study step types. For information about error estimation with time-dependent adaptation, see Error Indicator for the Time-Dependent Solver.

A common approach to adaptive finite elements is to use the dual weighted residual method (DWR). The method is based on a posteriori error estimates for a (goal) functional together with some adaptive approach for the mesh in space and time. The framework was originally developed in Ref. 1 and Ref. 2. For stationary problems or problems cast in a Galerkin formulation, the starting point is the following exact representation of the discretization error in a linear functional J:

where u is the exact primal solution, uh is the finite-element approximation of u, ρ is the weak residual of the problem, z is the exact dual solution corresponding to J, and zh is the finite-element approximation of z. The weak residual ρ is defined by

where v and are arbitrary elements in a function space V, F is a linear functional, and A is a bilinear functional. The exact primal solution u in V is defined by

and the approximate primal solution uh in the finite-element space Vh is thus defined by

The exact dual solution z in V is defined by

and the approximate dual solution zh in Vh is thus defined by

where the residual is computed by standard finite element method assembling (using numerical quadrature) for the higher-order finite-element space. This residual is then used to compute a normalized elementwise norm for each equation (here defined by the fields and their components). This technique is the same as when using mesh adaptation (see The Adaptive Solver Algorithms and Error Estimation). Also for the error estimation, the method separates the error contribution from different equations:

where j is an equation index and the mesh element K, and where the equations are defined from the field components.

where with the bar is the estimated maximum norm of the residual for the equation j and mesh element K, and is the mesh element volume. Furthermore,

where 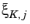is the estimated maximum norm of the error for the dual solution to equation j and mesh element K. Since the exact dual solution is often not known, the weight function z − πhz must be approximated by some method. For Lagrange basis functions, the default method uses the polynomial-preserving recovery (PPR) technique (built in through the ppr and pprint operators) to estimate the dual solution and thereby the error

where xl are a number of coordinates in the mesh element K. These coordinates are a union of Lagrange points and Gauss points. For both Lagrange and non-Lagrange basis functions, a different method that uses an interpolation-error estimate is supported. For basis functions of order p, this error estimate is

where h is the mesh element diameter, q (which is related to p) is the order of the interpolation error, Dq z<j> is a tensor of partial derivatives of total order q, and k denotes a vertex of mesh element K. For many element types, including Lagrange, the basis functions span a complete polynomial space of order p, and thus q = p + 1. For vector elements of type 1, q = p. 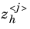The norm of the tensor of partial derivatives of order q is estimated as follows: For a given mesh vertex, a patch of surrounding mesh elements is formed, and a polynomial of degree q (in global coordinates, with the origin at the vertex) is fitted to the values of in a set of sampling points in these elements. In 2D, the polynomial in question is

and the corresponding estimate of the norm of the tensor of partial derivatives of order q is

where the sum is over the coefficients of highest degree (degree q). Finally, in the case of a geometric entity with lower dimension than the space (that is, a boundary or an edge), the PPR and interpolation-error methods are not supported. In this case, a less accurate method based on the gradient of the dual solution is used:

Ideally, since the error representation (Equation 20-1) is exact, the error estimate above has the potential of being very accurate. The method is not fail-safe, however. For example, the underlying PDE problem must be well-posed and its solution sufficiently regular. Sufficiently regular means that not only is the solution bounded in some norm, but also a number of derivatives need to be bounded in some norm. Well-posedness for the dual problem and sufficient regularity for the dual solution are also required.

The residual and dual weights (Equation 20-3 and Equation 20-4) for a component comp1.u are stored in dependent variables called comp1.res.u and comp1.dualw.u, respectively. The error variable is defined as the product of these and is accessible as comp1.err.u. These variables are accessible for plotting in plot nodes using the Expression as, for example, for a Solid Mechanics physics interface)
Component 1>Solid Mechanics>Error estimation>err.u - Error estimate u.

You can access the residual and dual weights directly through the dependent variable names. For a Stationary study step called stat (and similarly for a Frequency Domain study step), the total global error summed over all mesh elements is stat.errEst, and the error contribution from a variable comp1.q is comp1.stat.errEst.q. The error contribution from comp1.q can be evaluated under Results>Derived Values by adding a Global Evaluation node, and then under Expression selecting Global Definitions>Error estimation>stat.errEst - Error estimate global - Stationary. The error contribution from comp1.q can be evaluated by selecting Component1>Global Definitions>Error estimation>stat.errEst.q - Error estimate q. For fields using vector elements, the error estimates are done fieldwise and have a suffix _field in the variable name for the error (for example, err.E_field). For other cases, the estimates are done componentwise.