Local Time Stepping
The time step restriction is directly proportional to the smallest mesh element size. The CFL condition is normally too restrictive on highly graded meshes. On such a mesh, it is common that only few elements are small, yet these dictate the overall time step for the whole problem. As an example, think of a mesh with a small geometric feature somewhere or a mesh stemming from an adaptive computation.
In these cases one option is to use local time stepping, which allows the use of a larger time step based on the size of the majority of the elements. This is possible due to the element-wise nature of the DG scheme. The larger the spread is between the smallest mesh-element size and the ideal mesh-element size dictated by a points per wavelength argument, the more beneficial this technique is.
The basic problem with local time stepping, aside from stability issues, is to obtain high accuracy. Classical results only involve second order accuracy. This is not good enough for DG methods.
In order to perform local time stepping, the third order classical Adams-Bashforth (AB) method is implemented
(16-14)
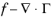
here, un is the solution at time tn, k is the time step, and R(un) the weak form of the DG scheme (compare to the weak formulation of Equation 16-13), which includes the numerical flux.
The basic idea with local time stepping is as follows. First, the elements are divided into groups, based on their size. Typically, the groups are constructed such that the time steps k, k/2, k/4, and so forth are stable time steps for each group of elements and where any coupling between groups is disregarded. This allows for easy synchronization of the solution at every full step. The right-hand-side vectors
, , and
are expensive to compute, thus these are naturally stored from previous time steps, so for each group of DOFs, their own history of right-hand sides are stored.
The main idea with local time stepping is to match the different groups with their own time step and thus save computational resources.
•
References for the Solution Operation Nodes and Solvers
•
Introduction to Solvers and Studies