Derivation of the Weak Form of the Wave Form PDE

Using About Auxiliary Equation-Based Nodes it is possible to solve one or several first-order wave equations; that is, PDEs of the form

where u is the unknown, da the mass coefficient, f the source, and Γ the flux vector, which generally depends on u.

The numerical method consists of a discontinuous Galerkin method in space in combination with explicit Runge-Kutta time stepping. This combination of space and time discretization is particularly well-suited for wave problems due to a favorable CFL condition. This is true even when using a high-order polynomial ansatz for u.

In order to derive the weak form underlying the DG method, let

denote a mesh of the domain

, with

denoting a single element. On this mesh, let V be the broken space

with

denoting the space of all polynomials of degree at most s on

	These functions are continuous in the interior of each mesh element, but generally discontinuous across the element boundaries.

A basis for V is given by the nodal discontinuous Lagrange shape functions shhwdisc (see Discontinuous Lagrange (shdisc) and Nodal Discontinuous Lagrange Elements (shhwdisc) in the COMSOL Multiphysics Programming Reference Manual. This basis is tailor made for this type of discontinuous Galerkin method, and it has nearly optimal interpolation properties.

The starting point for deriving a weak form is to multiply the PDE with a test function

and integrate over the domain, to yield

The next step is to integrate by parts. Some care must be taken, since the integrands v and u are discontinuous functions across element boundaries and only continuous in the interior of each element. Therefore, the integrals are first written as a sum over the elements and then integration by parts is done on each element, which gives

where n is the outward unit normal on the element. Further,

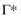
is the so-called numerical flux, which defines the flux vector on each element boundary. The flux vector is usually discontinuous because it depends on u.

The numerical flux defines how adjacent elements are connected and how continuous u is. Different definitions of the numerical flux lead to different variants of discontinuous Galerkin methods.

The numerical flux implemented in COMSOL Multiphysics is the global Lax-Friedrichs flux:

where the angles

and brackets

are the average and jump operators, respectively. Thus, on each element boundary, this flux is simply the average of the flux on the two adjacent elements sharing the face, plus a penalty on any jumps of the solution. The penalty is needed for stability and is proportional to the parameter τ, which is assumed to be constant over the whole domain Ω. The normal vector n is a, from the element, outward pointing normal vector. The jumps are defined as

where u_ is the inside values and u+ is the outside value. So it is the element’s value minus the other element’s value. The multiplication is an outer product in the case of a vector quantity u.

Using the definition of the Lax-Friedrichs flux, the weak form is obtained

It is also possible to specify a general numerical flux g.

What makes this discontinuous Galerkin method particularly attractive for explicit time stepping is the fact that the term

yields a block diagonal mass matrix, where each block only involves the degrees of freedom on each element. As a consequence, there is no need to invert or solve any linear system involving the global mass matrix. The inverse of the global mass matrix simply amounts to inverting the local mass matrix on each element. This is efficiently done using high performance routines such as BLAS or LAPACK.

A known drawback with explicit time stepping is the requirement on the time step, which has to be very small in order to obtain a stable numerical method. This is referred to as the CFL condition, which relates the largest possible time step k to the smallest mesh size h. For wave equations with unit wave speed, the CFL condition takes the form

where p is the order of the shape functions and C a generic constant, typically 0.25.

As implemented in COMSOL Multiphysics, the nodal discontinuous Lagrange shape functions are the only set of shape functions defined for this interface. The associated element order can be chosen from the list. The highest available order is four, and the default order is two.