Here εp (dimensionless) is the porosity, and the vector
ui should now be interpreted as the volumetric flux of phase
i (SI unit m
3/(m
2·s) or m/s). The volumetric fluxes are determined using the extended Darcy’s law (
Ref. 2)
where κ denotes the permeability (SI unit: m
2) of the porous medium,
g the gravitational acceleration vector (SI unit m/s
2), and
μi the dynamic viscosity (SI unit: kg/(m·s)),
pi the pressure field (SI unit: Pa), and
κri the relative permeability (dimensionless) of phase
i, respectively.
One phase pressure can be chosen independently, which in the Phase Transport in Porous Media interface is chosen to be the phase pressure,
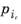
, of the phase computed from the volume constraint, and the other phase pressures are defined by the following
N − 1 capillary pressure relations:
Substituting Equation 6-100 into
Equation 6-99, and using the volume constraint in
Equation 6-121, we arrive at the following
N − 1 equations for the phase volume fractions
si, (
i ≠ ic) that are solved in the
Phase Transport in Porous Media interface: