You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Phase Properties node has the material properties settings for the pure continuous and dispersed phases. It also has settings for the viscosity models for each of the two interpenetrating phases and the drag model. When the dispersed phase consists of solid particles, it also has settings for the solid pressure model.
By default, the Temperature model input is set to
Common model input, and the temperature is controlled from
Default Model Inputs under
Global Definitions or by a locally defined
Model Input. If a Heat Transfer interface is included in the component, it controls the temperature
Common model input. Alternatively, the temperature field can be selected from another physics interface. All physics interfaces have their own tags (
Name). For example, if a Heat Transfer in Fluids interface is included in the component, the
Temperature (ht) option is available for
T.
You can also select User defined from the
Temperature model input in order to manually prescribe
T.
The default Absolute pressure pA is
p+pref, where
p is the dependent pressure variable from the Navier–Stokes or RANS equations, and
pref is from the user input defined at the physics interface level. When
pref is nonzero, the physics interface solves for a gauge pressure. If the pressure field instead is an absolute pressure field,
pref should be set to 0.
The Absolute pressure field can be edited by clicking
Make All Model Inputs Editable (

) and entering the desired value in the input field.
Select the materials to use for the material properties of the continuous phase and the dispersed phase respectively (when they are defined to take their values From material). By default, the default material used for the
Continuous phase is the
Domain material. This corresponds to the material currently applied to the domain in question. The
Dispersed phase uses
None per default. A valid material must be selected instead.
Other materials present can be selected from the Continuous phase or
Dispersed phase list in order to use that material’s properties for the liquid or gas, respectively.
The default Density, continuous phase ρc (SI unit: kg/m
3) uses values
From material. For
User defined enter another value or expression.
The default Dynamic viscosity, pure continuous phase μc (SI unit: Pa·s) uses values
From material. The value of the viscosity is then the value defined for the material selected in the
Materials section for the continuous phase. For
User defined define a different value or expression.
The default Density, dispersed phase ρd (SI unit: kg/m
3) uses values
From material. For
User defined enter another value or expression.
Enter a value or expression for the Diameter of particles/droplets dd (SI unit: m). The default is 10
−3 m (1 mm).
|
|
The Dynamic viscosity, pure dispersed phase μd (SI unit: Pa·s) field is available when Liquid droplets/bubbles is selected as the Dispersed phase in The Euler-Euler Model Interfaces.
The default uses values From material. The value of the viscosity is then the value defined for the material selected in the Materials section for the dispersed phase. For User defined define a different value or expression.
|
Select a model for the Mixture viscosity —
Krieger type (the default),
Volume average (available for liquid droplets and bubbles) or
User defined. Krieger type is appropriate for dispersed phases that do not form any pure phase regions. Volume average is more appropriate when the dispersed phase effectively can become the only phase in some regions.
|
•
|
For Krieger type, select an option for Maximum packing concentration. The default is to use 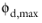 = 1.0 for droplets and bubbles and 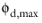 = 0.62 for particles. Select User defined to enter another value or expression for 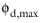 .
|
|
•
|
For User defined enter a value or expression for the Mixture viscosity. The default expression corresponds to the Krieger type viscosity with maximum packing equal to 0.62.
|
Select a Dynamic viscosity model, continuous phase —
Mixture viscosity (default),
Pure phase value or
User defined. The
Mixture viscosity option is appropriate when the maximum packing is controlled by the mixture viscosity. The
Pure phase value option is more appropriate if the maximum packing is controlled in some other way, for example by solid pressure. Select
User defined to enter an expression for the
Dynamic viscosity model, continuous phase.
Select a Dynamic viscosity model, dispersed phase —
Mixture viscosity (default),
Pure phase value (available for bubbles and droplets),
Gidaspow (available for solid particles) or
User defined. The
Gidaspow model prescribes
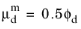
which basically prescribes a small value for
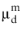
and should be combined with a solid pressure model.
The models are described in The Euler–Euler Model Equations. When the dispersed phase corresponds to
Solid particles, the
Schiller-Naumann,
Hadamard-Rybczynzki, Ishii-Zuber,
Gidaspow,
and
Haider-Levenspiel models are available. For
Liquid droplets/bubbles, the
Schiller-Naumann,
Hadamard-Rybczynzki, Ishii-Zuber,
Tomiyama et al. models are available. Select the
User-defined drag coefficient option to specify an expression for the drag coefficient
CD.
|
•
|
The Schiller-Naumann is valid for dispersed, rigid spheres and can be used for particle Reynolds numbers less than approximately 2.5·10 5. The Schiller-Naumann model is a general purpose model for diluted flows.
|
|
•
|
The Hadamard-Rybczynzki is appropriate for diluted flows at low Reynolds numbers.
|
|
•
|
The Ishii-Zuber model can for solid particles be regarded as a generalization of the Schiller-Naumann model in that it can be used also for dense flows. For droplets and bubbles, the Ishii-Zuber model also takes deformation of the fluid particles into account. The deformation depends on the Surface tension coefficient, σ. Use a predefined expression, select Library coefficient, liquid/gas interface or Library coefficient, liquid/liquid interface. Then select an option from the list that displays below (for example, Water/Air, Glycerol/Air and so forth). For User defined enter a value or expression for the surface tension coefficient σ (SI unit: N/m).
|
|
•
|
The Gidaspow model describes the drag force coefficient for dispersed phase flows for all concentrations of the dispersed solid, including high concentrations.
|
|
•
|
The Haider-Levenspiel model describes non-spherical particles for low and moderate particle Reynolds numbers. Enter a value between 0 and 1 for the Sphericity Sp (dimensionless).
|
|
•
|
The Tomiyama et al. model describes the drag for diluted droplets and bubbles for any particle Reynolds number. The correlation is available in three versions, Pure fluid, Slightly contaminated fluid and Contaminated fluid. The Tomiyama et al. model depends on the Surface tension coefficient, σ that is selected in the same way as for the Ishii-Zuber model.
|
This section is available when Solid particles is selected as the
Dispersed phase in
The Euler-Euler Model Interfaces. Select a
Solid pressure model ∇ps.
|
•
|
The No solid pressure (the default) disables solid pressure and leaves the collision to be described by a mixture viscosity. This option is appropriate for solid suspension, typically solids suspended in liquids.
|
|
•
|
The other options, Gidaspow-Ettehadieh, Gidaspow, Ettehadieh and User defined modulus of elasticity describes particle-particle interaction for dispersed solids, typically solid particles in gas flows. These options should be combined with the Gidaspow model or a small user defined value for 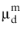 .
|
|
•
|
For User defined modulus of elasticity enter an expression for the Modulus of elasticity, G (SI unit: N/m 2).
|
When the Mixing length limit lmix, lim is set to
Automatic, the mixing length limit is evaluated as the shortest side of the geometry bounding box. If the geometry is, for example, a complicated system of slim entities, this measure can be too high. In such cases, it is recommended that the mixing length limit is defined manually. Select
Manual to enter a different value or expression.