Here 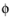 (dimensionless) denotes the phase volume fraction, ρ
(dimensionless) denotes the phase volume fraction, ρ (SI unit: kg/m
3) is the density,
u (SI unit: m/s) the velocity of each phase, and
mdc is the mass transfer rate from the dispersed to the continuous phase (SI unit: kg/(m
3·s)). The subscripts
c and
d denote quantities relating to the continuous and the dispersed and phase, respectively. The following relation between the volume fractions must hold
If Equation 6-54 and
Equation 6-53 are added together, a continuity equation for the mixture is obtained:
Here p (SI unit: Pa) is the mixture pressure, which is assumed to be equal for the two phases. In the momentum equations the viscous stress tensor for each phase is denoted by
τ (SI unit: Pa),
g (SI unit: m/s
2) is the vector of gravitational acceleration,
Fm (SI unit: N/m
3) is the interphase momentum transfer term (that is, the volume force exerted on each phase by the other phase),
F (SI unit: N/m
3) is any other volume force term, and
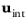
is the interphase velocity (SI unit: m/s).
where ps (SI unit: Pa) is the solid pressure.
where 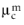 and
and 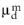 (SI unit: Pa·s) are the dynamic viscosity model of the respective phase. Observe how the viscous terms in equation Equation 6-56
(SI unit: Pa·s) are the dynamic viscosity model of the respective phase. Observe how the viscous terms in equation Equation 6-56 and
Equation 6-57 appear with their volume fractions outside the divergence operators. The equations can also be derived so that the terms read
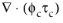
and
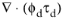
instead (see for example
Ref. 4 or
Ref. 5). It depends on exactly how the derivation is carried out. formulation in
Equation 6-56 and
Equation 6-57 are so that the momentum equation can be divided by
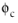
and
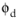
respectively as described below.
Here 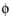 d,max
d,max is the maximum packing limit, by default 0.62 for solid particles.
Equation 6-62 can be applied when
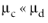
. An extension of
Equation 6-62 can be applied for liquid droplets/bubbles:
This is consistent with the requirement that 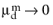 when
when 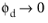 (Ref. 9
(Ref. 9), but in practice it can suffice with any small enough, nonzero value.
In all the equations, Fm denotes the interphase momentum transfer, that is the force imposed on one phase by the other phase. Considering a particle, droplet, or bubble in a fluid flow, it is affected by a number of forces, for example, the drag force, the added mass force, the Basset force, and the lift force. The most important force is usually the drag force, especially in fluids with a high concentration of dispersed solids, and hence this is the predefined force included in the Euler–Euler model. The drag force added to the momentum equation is defined as:
where β is a drag force coefficient and the slip velocity is defined as
The drag force coefficient, β, is for solid particles often written as (
Ref. 2)
which is consistent with a vanishing β if
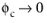
. All drag force models except Gidaspow are based on
Equation 6-67 for solid particles and on
Equation 6-68 for bubbles and droplets.
In the above equations, dd (SI unit: m) is the dispersed particle diameter, and
Cd is the drag coefficient for a single dispersed particle. The drag coefficient is in general a function of the particle Reynolds number
The Ishii-Zuber model (Ref. 10) can for solid particles be regarded as a generalization of the Schiller-Naumann model. For solid particles it can be formulated as
and Rem is a Reynolds number based on the mixture viscosity
The Ishii-Zuber model is formulated with the assumption that 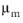 is described by a Krieger type model (Equation 6-62
is described by a Krieger type model (Equation 6-62 for solids or
Equation 6-63 for droplets and bubbles). The dependence on
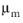
means that the Ishii-Zuber model is valid also for dense suspensions.
where in turn g is the gravitational constant and
σ is the surface tension coefficient. The Eötvös number relates surface tension forces to gravitational forces. The second, “distorted” regime ends when hydrodynamic instabilities prevents the drag from increasing further and the distorted regime is capped by the following value:
where A,
B,
C,
and
D are empirical correlations of the particle sphericity (see
Slip Velocity Models for further details).
The Tomiyama et al. (
Ref. 11) provided three correlations for diluted bubbles and droplets. The correlation for purified fluids read
Fluid pure enough for Equation 6-80 to be valid is typically only achievable in laboratory environments. Even small amounts of surface-active impurities can collect at the droplet/bubble interface and cause a surface tension gradient which resists surface movement. The correlation for slightly contaminated fluids therefore prescribe a slightly higher drag coefficient:
For fluid-solid mixtures where 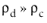
, for example solid particles in gas flow, a model for the solid pressure,
ps in
Equation 6-60,
is needed. The solid pressure models the particle interaction due to collisions and friction between the particles. The solid pressure model implemented uses a gradient diffusion based assumption:
where the empirical function G can be though of as a modulus of elasticity or powder modulus. A common form for
G is (
Ref. 5)
in Equation 6-59. Also,
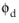
is a degree of freedom and can therefore, during computations, obtain nonphysical values in small areas. This can, in turn, lead to nonphysical values of material properties such as viscosity and density. To avoid these problems, the implementation uses the following regularizations:
Note however that the continuity equation, Equation 6-55, uses
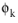
without regularization in order to guarantee mass conservation.