In turbulent flow the reaction rate is significantly affected by the turbulence. Turbulent fluctuations can increase the reaction rate due to the increased mixing, but it can also quench it through removal of species or the heat required for ignition. The interaction between the flow and the reactions can be quantified through the Damköhler number Da:

which compares the time scale of the largest turbulent flow structures (the integral time scale), to the chemical time scale. In the limit of large Damköhler numbers Da >> 1, the reactive time scale is significantly smaller than that of the turbulence. In this regime the inner structure of a reaction zone is thin enough not to be affected by turbulence. The reacting regions are, however, convected and wrinkled by the turbulence. In this case the global reaction rate is proportional to the chemical reaction rate times the surface of the reacting regions. In the limit of small Damköhler numbers Da << 1, the chemical time scale is much larger than that of the turbulent flow. In this case the global reaction rate is controlled by the chemistry, while the turbulence acts by continuously mixing the species. This regime is referred to as a “perfectly stirred reactor”.

where νi denotes the species stoichiometric coefficient, Mi the molar mass (SI unit: kg/mol), and rMVC,i is the reaction rate from Equation 8-65 using mean quantities.

This is referred to as mean value closure of the turbulent reaction rate, and corresponds to keeping the first term in a Taylor series expansion of the turbulent reaction rate following a Reynolds decomposition of the fluctuating variables (Ref. 5). The mean value closure is directly applicable in the perfectly-stirred-reactor limit (Da << 1). In this case the turbulence is able to mix the species in the sense of changing the mean concentration, but the turbulent fluctuations do not affect the chemical reaction rate. The mean value closure is also applicable in the limit of low turbulence levels since the turbulent fluctuations tend to zero as the laminar flow regime is approached.

The eddy-dissipation model for the mean reaction rate originally developed by Magnussen and Hjertager (Ref. 6) for non-premixed combustion. Using this reaction model, the mean production rate of species i is defined as:

The model assumes that both the Reynolds and Damköhler numbers are sufficiently high for the reaction rate to be limited by the turbulent mixing time-scale τT. The reaction can hence at most progress at the rate at which fresh reactants are mixed, at the molecular level, by the turbulence present. Furthermore the reaction rate is limited by the deficient reactant; the reactant with the lowest local concentration. When the model parameter β is finite, the existence of product species is also required for reaction, modeling the activation energy required for reaction (ignition). For gaseous non-premixed combustion the model parameters have been found to correspond to (Ref. 6):

For liquid reactions it is recommended that the model parameters are calibrated against experimental or simulation data. Using a mix of the mean value closure and a modified version of the eddy-dissipation model Bakker and Fasano (Ref. 7) found the following parameter values

to give good results for a competitive reaction pair when compared with experimental results.

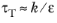
A common approximation for the turbulence mixing time-scale τT is (Ref. 5). Due to realizability constraints, a more accurate approximation is however

for 3D and 2D axisymmetry. Equation 8-69 is directly applicable to the k-ε model. For the k-ω and SST turbulence models, Equation 8-69 reads

Equation 8-69 is used also for the low-Reynolds k-ε model even though k/ε is not actually the turbulence mixing time scale. To obtain a consistent turbulence mixing time scale for low-Reynolds k-ε, k/ε needs to be multiplied by a damping function that goes to zero at solid walls. Ref. 5 does however notice that τT is not a relevant time scale close to walls since it is too small. The damping function is therefore neglected in the eddy-dissipation model.