The inelastic behavior of materials is often described by the rate of the inelastic quantity, especially if the behavior is time dependent and nonlinear. For example, Elastoplastic Material Models, Linear Viscoelasticity, Creep and Viscoplasticity all describe material models that are implemented in dedicated features. 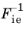The Inelastic Strain Rate node provides functionality to specify a general expression for the rate of inelastic deformation, entered either as strain tensor εie; deformation gradient Fie; deformation gradient inverse ; or stretch λie. The user defined expression can be a function of any variable in the model.

Given a generic inelastic quantity Uie, the feature sets up and solves the following type of distributed ODE

where t is the time, u is the displacement, and f(t, u, Uie,...) is a user defined expression. Equation 3-83 is also subjected to the initial condition

The distributed ODE in Equation 3-83 is integrated in time to compute the value of the inelastic quantity Uie at each time step. This can be done using any of the following methods:

The Backward Euler method is used to discretize Equation 3-83 as

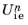
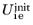
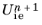
where n+1 indicates the current time step, and Δt is the time step. The inelastic quantity at the previous time step is stored as internal state variables, their initial value is given by . Equation 3-84 defines a system of nonlinear equations that is solved locally at each Gauss point for using Newton’s method.

For Domain ODEs, Equation 3-83 is converted to weak-form and solved as part of the general initial-boundary value problem. The components of the inelastic quantity Uie are here treated as a degrees-of-freedom of the model.