You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Viscoelastic materials have a time-dependent response even if the loading is constant in time. Many polymers and biological tissues exhibit this behavior.
Linear viscoelasticity is a commonly used approximation where the stress depends linearly on the strain and its time derivatives (strain rate). Also, linear viscoelasticity deals with the
additive decomposition of stresses and strains. It is usually assumed that the viscous part of the deformation is incompressible so that the volumetric deformation is purely elastic.
where the elastic strain tensor εel = ε − εinel represents the total strain minus initial and inelastic strains, such as thermal strains.
The elastic strain tensor εel can in the same way be decomposed into volumetric and deviatoric components
In case of geometric nonlinearity, σ represents the second Piola–Kirchhoff stress tensor and
εel the elastic Green–Lagrange strain tensor.
For viscoelastic materials, the deviatoric stress σd is not linearly related to the deviatoric strain
εd but it also depends on the strain history. It is normally defined by the hereditary integral:
The function Γ(
t) is called the
relaxation shear modulus function (or just
relaxation function) and it can be found by measuring the stress evolution in time when the material is held at a constant strain.
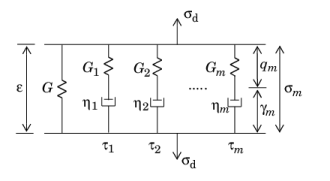
Hence, G is the stiffness of the main elastic branch,
Gm represents the stiffness of the spring in branch
m, and
τm is the
relaxation time constant of the spring-dashpot pair in branch
m.
The relaxation times τm are normally measured in the frequency domain, so the viscosity of the dashpot is not a physical quantity but instead it is derived from stiffness and relaxation time measurements. The viscosity of each branch can be expressed in terms of the shear modulus and relaxation time as
The auxiliary strain variable qm is introduced to represent the extension of the corresponding abstract spring, and the auxiliary variables
γm = ε − qm represent the extensions in the dashpots.
The shear modulus of the elastic branch G is normally called the
long-term shear modulus, or
steady-state stiffness, and it is often denoted with the symbol
G∞. The instantaneous shear modulus
G0 is then defined as the long-term shear modulus plus the sum of the stiffnesses of all the viscoelastic branches
Sometimes, the relaxation function Γ(
t) is expressed in terms of the instantaneous stiffness and relative weights, so that the Prony series is given as
|
|
The long-term shear modulus G is given in the parent material model (e.g. Linear Elastic Material). If your material data consists of the instantaneous shear modulus G0 and the weights wm, you can convert the data using the formulas above.
In the parent Linear Elastic Material, you can enter the long-term elastic data in any form, for example in terms of Young’s modulus, E, and Poisson’s ratio, ν. It will then be converted to the corresponding shear modulus G internally.
|
The total stress in Hooke’s law (Equation 3-15) is then augmented by the viscoelastic stress
σq
(3-26)
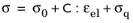
The auxiliary variable γm is a symmetric isochoric (volume preserving) strain tensor, which has as many components as the number of strain components of the problem class. Since the stress per branch is written as
the auxiliary variables γm can be computed by solving the ODE
(3-27)
so that Equation 3-27 can equivalently be written as
(3-28)
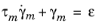
The viscoelastic strain variables, γm, are treated as additional degrees of freedom (DOFs). The shape functions are chosen to be one order lower than those used for the displacement field, because these variables add to the strains and stresses computed from displacement derivatives. Alternatively,
Equation 3-41 can be solved using a
Local Time Integration algorithm.
|
|
The viscoelastic strain variables γm are called for instance solid.lemm1.vis1.ev1_11, where solid is the tag of the physics interface, lemm1 is the tag of the linear elastic material, and vis1 is the tag of the viscoelasticity node. The trailing numbers indicate the branch number and the strain tensor indices.
|
where εel,vol is the elastic volumetric strain, and the auxiliary variables
evol,m represent the volumetric deformation per branch. These are computed by solving the ODE
where τm is the relaxation time per branch.
|
|
The volumetric viscoelastic strain variables evol,m are called, for example, solid.lemm1.vis1.evvol1, where solid is the tag of the physics interface, lemm1 is the tag of the linear elastic material node, and vis1 is the tag of the viscoelasticity node. The trailing number represents the branch number (i.e. the first branch in this case).
|
When the frequency band of interest is bounded by two cutoff frequencies, flower and
fupper, it is possible to prune viscoelastic branches that have relaxation times such as
Branches with short relaxation times τk represent the response of the viscoelastic material to high frequency excitations. When the external loads represent excitations bounded by an upper frequency
fupper, it is possible to prune branches with relaxation times that fulfill the relation
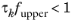
. These branches are grouped into an equivalent branch, with relaxation time and stiffness such as
Viscoelastic branches with relaxation times τk such that

are grouped into an equivalent branch forming the low frequency cutoff. The stiffness and relaxation time for the equivalent branch are computed from
The dissipated energy density rate (SI unit: W/m
3) in each dashpot
m is
The Maxwell model is a simplification of the generalized Maxwell model with only one spring-dashpot branch:
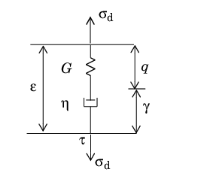
The generalized Kelvin–Voigt model is used to simulate the viscoelastic deformation in a wide range of materials such as concrete, biological tissues and glassy polymers.
Just as for the generalized Maxwell model, the deviatoric strain εd is not linearly related to the deviatoric stress
σd, but it also depends on the strain history. It is normally defined by the hereditary integral:
The function ψ(
t) is called the
compliance function (also called
creep compliance or
creep function) and it can be found by measuring the strain evolution in time when the material is held at a constant stress.
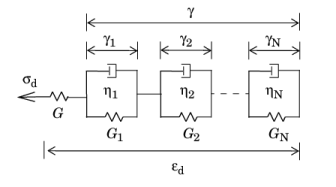
Here, G is the stiffness of the main elastic branch,
Gm represents the stiffness of the spring in element
m, and
τm is the
relaxation time constant of the spring-dashpot pair in branch
m. The compliance
J in the pure elastic branch is related to the shear modulus by
The relaxations time τm is normally measured in the frequency domain, so the viscosity of the dashpot is not a physical quantity but instead it is derived from stiffness and relaxation time measurements. The viscosity in each branch can be expressed in terms of the stiffness or compliance modulus and relaxation time as
The auxiliary strain variables γm are introduced to represent the extension of the corresponding Kelvin–Voigt element. Since the elements are arranged in series, the total viscoelastic strain is given as the sum of the auxiliary strains
(3-29)
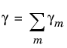
The deviatoric stress σd in the pure elastic branch is the same as in all the Kelvin–Voigt elements
(3-30)
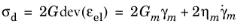
The auxiliary strain variables γm represent a symmetric isochoric (volume preserving) strain tensor, which has as many components as the number of strain components of the problem class.
The stress in each element m is given by the sum of the stresses in the spring and dashpot arranged in parallel
Here, γm is the strain in the element
m, and
ηm = τmGm is the viscosity. The auxiliary variables
γm are computed by solving the ODE
(3-31)

The compliance of the elastic branch, J = 1/G, is normally called the
instantaneous compliance, and it is often denoted with the symbol
J0. This gives the equivalent stiffness when the material is loaded by an abrupt load much faster than the shortest relaxation time of any branch.
The long-term compliance J∞ is defined as the instantaneous compliance plus the sum of the compliances of the viscoelastic branches
Sometimes, the compliance function ψ(
t) is expressed in terms of the instantaneous compliance
J and relative weights
wm, so that the Prony series reads
The dissipated energy density rate (SI unit: W/m
3) in each branch
m is given by the dissipation in the dashpot
The Kelvin–Voigt viscoelastic model is represented by a spring connected in parallel with a dashpot:
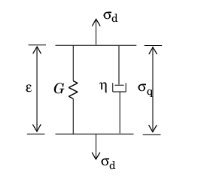
(3-32)
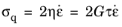
The relaxation time relates the viscosity and shear modulus by η = τG. The equivalent shear modulus is used in case of an anisotropic linear elastic material.
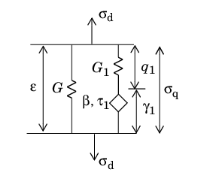
The standard linear solid model, also called
SLS model,
Zener model, or
three-parameter model, is a simplification of the generalized Maxwell model with only one spring-dashpot branch:

The auxiliary strain tensor γ1 is computed by solving by the ODE
The long-term shear modulus G∞ = G is given in the parent
Linear Elastic Material, and the instantaneous stiffness is given by
G0 = G+G1.
The Burgers model consists of a Maxwell (spring-dashpot) branch in series with a Kelvin–Voigt branch. The rheological representation of this material model is shown in
Figure 3-6:
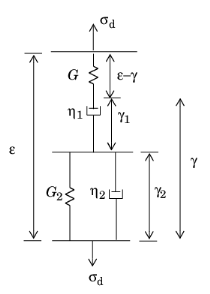
where the shear modulus G is taken from the parent Linear Elastic material.
Typically, the rheology of viscoelasticity models consists of springs and dashpots arranged in series and in parallel. Using the framework of fractional calculus, the constitutive equations of linear viscoelasticity can be generalized with a new type of element, named
spring-pot (
Ref. 38). In some cases, viscoelasticity models with fractional derivatives have shown to better match experimental data.

The fractional order β takes a value between
0 < β < 1. For
β = 0, the parameter
p plays the role of a stiffness in a spring, and for
β = 1 the parameter plays the role of the viscosity in a dashpot. The SI unit for such material parameter would be Pa·s
β.
For a standard spring-dashpot branch, the relaxation time is given by the ratio of viscosity and stiffness, τ = η/G. Equivalently, the relaxation time
τ for a branch with a spring and a spring-pot element in series is derived from
Thus, p = τβ/G, and the stress-strain relationship in the spring-spring-pot system reads
For The Generalized Maxwell Model with fractional derivatives, all dashpots are replaced with spring-pot elements. The rheological representation of this material model is shown in
Figure 3-9 
where Gm,
τm and
βm are the shear modulus, relaxation time and fractional order of branch
m, respectively. Storage and loss moduli are defined as the real and imaginary part of the complex shear modulus.
The relaxation time τ for a spring and a spring-pot element in parallel is derived from
so p = τβ/G, and the stress-strain relationship in the Kelvin–Voigt element reads
The complex-valued compliance of the Kelvin–Voigt element with fractional time derivative reads
For The Generalized Kelvin–Voigt Model with fractional derivatives, all dashpots are replaced with spring-pot elements.
where Gm,
τm and
βm are the shear modulus, relaxation time and fractional order of element
m, respectively. Storage and loss moduli are defined as the real and imaginary part of the complex shear modulus
In the rheological representation of the Standard Linear Solid Model with fractional derivatives, the dashpot is replaced with a spring-pot element.
here, γ1 is the strain in the spring-pot element. In frequency domain this equation translates to
Using the relaxation time τ = (p/G1)1/β, this reads
where Gq = G1(jωτ)β/(1+(jωτ)β) is the complex shear modulus of the spring-pot branch.
In the rheological representation of The Burgers Model with fractional derivatives, the dashpots are replaced with a spring-pot elements. The rheological representation of this material model is shown in
Figure 3-13:

here, γ1 is the strain in the spring-pot element. In frequency domain, and using the relaxation times
τ1 = (p1/G)1/β1, this equation translates to
here, γ2 is the strain in the second spring-pot element. In frequency domain, and using the relaxation time
τ2 = (p2/G2)1/β2, this equation reads
where D is the constitutive matrix computed from the material data, and
Dc is the complex constitutive matrix used to compute the viscoelastic stresses.
For many polymers, the viscoelastic properties have a strong dependence on the temperature. A common assumption is that the material is thermorheologically simple (
TRS). In a material of this class, a change in the temperature can be transformed directly into a change in the time scale. The reduced time is defined as
where αT(
T) is a temperature-dependent
shift function.
Think of the shift function αT(
T) as a multiplier to the viscosity in the dashpot in the Generalized Maxwell model. This multiplier shifts the relaxation time, so
Equation 3-28 for a TRS material is modified to
The first step to compute the shift function αT(
T)
consists of building a
master curve based on experimental data. To do this, the curves of the viscoelastic properties (shear modulus, Young’s modulus, and so forth) versus time or frequency are measured at a reference temperature
Tref. Then, the same properties are measured at different temperatures.
The shift value of each curve, with respect to the master curve obtained at the temperature Tref, defines the shift factor
αT(
T). The constants
C1 and
C2 are material dependent and are calculated after plotting
log(
αT) versus
T − Tref.
Since the master curve is measured at an arbitrary reference temperature Tref, the shift factor
αT(
T) can be derived with respect to any temperature, and it is commonly taken as the shift with respect to the glass transition temperature. The values
C1 =
17.4 and
C2 =
51.6 K are reasonable approximations for many polymers at this reference temperature.
Below the Vicat softening temperature, the shift factor in polymers is normally assumed to follow an Arrhenius law. In this case, the shift factor is given by the equation
here, a base-e logarithm is used, Q is the activation energy (SI unit: J/mol), and
R is the universal gas constant.
here, a base-e logarithm is used, Q is the activation energy (SI unit: J/mol),
R is the universal gas constant,
T is the current temperature,
Tref is a reference temperature,
χ is a dimensionless activation energy fraction, and
Tf is the so-called
fictive temperature. The fictive temperature is given as the weighted average of partial fictive temperatures.
Here, wi are the weights and
Tfi are the partial fictive temperatures. The partial fictive temperatures are determined from a system of coupled ordinary differential equations (ODEs) which follow Tool’s equation
here, λ0i is a structural relaxation time.
The instantaneous shear modulus G0 is defined as the sum of the stiffness of all the branches
Equation 3-26 and
Equation 3-28 are then simplified to
where the shear storage modulus G’ and the
shear loss modulus G” are defined for the generalized Maxwell model as
The direct use of frequency-dependent shear or bulk moduli, as described in Frequency Domain Analysis and Damping, leads to a nonlinear eigenvalue problem. COMSOL Multiphysics solves such nonlinear problems by expanding all nonlinear expressions with quadratic polynomials around a
frequency linearization point which you can specify in the
Eigenvalue Solver node. The linearized eigenvalue problem then reads
where ωL is the angular frequency at the linearization point. Thus, the solution of the linearized system of equations depends on the choice of the linearization frequency
ωL.
The viscoelastic strain variables, γm, are treated as additional degrees of freedom (DOFs), and contribute to the damping and stiffness matrices of the coupled system of equations.
For the The Generalized Maxwell Model and the
Standard Linear Solid Model it is possible to use a local time integration algorithm for time dependent analysis. By using this algorithm, the degrees-of-freedom related to viscoelasticity are treated as internal state variables, which makes the overall solution more efficient and also leaner in terms of memory usage. The implemented algorithm is based on the method originally suggested in
Ref. 21, and it is schematically described in the following.
(3-33)
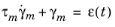
where γm is the viscoelastic strain in the branch. The exact solution to
Equation 3-33 is
(3-34)
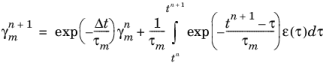
By assuming that the strain ε(
t) varies linearly within each time increment, the integral in
Equation 3-34 is analytically computed, so the viscoelastic strain at increment
n+1 reads
(3-35)

All variables in Equation 3-35 evaluated at increment
n are stored as internal state variables, and the equation can be applied to each branch of the Generalized Maxwell model. The same implementation is also used for the single branch in the Standard Linear Solid model.