Gaussian Beam Incident at the Brewster Angle

For a plane wave incident at an interface between two different media, there exists an angle of incidence for which there is no reflectance if the incident wave is polarized in the plane of incidence. The angle, for which the reflectance is zero, is called the Brewster angle.

Figure 1 shows an incident wave being reflected and refracted at the interface between the two media. The polarization component polarized in the plane of incident (the plane spanned by the wave vector of the incident wave and the normal to the interface) is not reflected. This polarization component is called the p-polarization.

The polarization component orthogonal to the plane of incidence (the s-polarization) is both reflected and refracted.

Figure 1: The figure shows the incident, reflected and refracted waves. At the Brewster angle αB the wave polarized in the plane of incidence is only refracted and not reflected.

At the Brewster angle, the incident p-polarized wave creates a polarization in the second medium (where the refracted wave is propagating) with the components in the propagation direction of the reflected wave. Because this is a longitudinal polarization for the reflected wave, and not a transverse polarization, it is clear that this polarization cannot excite a reflected wave.

Referring to the angles defined in Figure 1, write Snell’s law as

(1)

where n1 and n2 are the refractive indices above and below the interface, respectively.

Equation 1 results in the Brewster angle definition

From the Fresnel Equations Application Libraries example, the reflectance for the s-polarization at the Brewster angle is given by

(2)

This model does not use plane waves, but Gaussian beams (see for instance the Second Harmonic Generation of a Gaussian Beam Application Libraries model for a discussion about Gaussian beams). However, because the spot size for the beam is much larger than the wavelength, the plane wave relations above are good approximations also for the Gaussian beams.

Model Definition

This model demonstrates the use of the User defined phase specification, when using the Electromagnetic Waves, Beam Envelopes interface. Secondly, the model shows how the Matched Boundary Condition feature can be used to absorb waves that propagate toward a boundary in a direction different from the boundary’s normal direction. Here, a Scattering Boundary Condition feature is not an option, as that feature only absorbs waves propagating at or close to the normal direction to the boundary normal. A second alternative would be to use a Perfectly Matched Layer (PML) domain. However, in that case, extra degrees of freedom would have to be included for the PML domain. Thus, the Matched Boundary Condition feature is the best feature to use for absorbing beams propagating in directions that are not in the normal direction to the boundary.

The User defined phase is specified by defining parameters for the wave vectors of the forward- and backward-propagating waves in the two different media and then defining phase variables, phi1 and phi2, for the two waves in the two different media, as shown in Table 1.

Table 1: phase variable definition.
variable	expression
phi1	k1x_NNx+k1y_NNy
phi2	k2x_NNx+k2y_NNy

Here NN should be replaced by air and glass, respectively, for the two media.

As the geometry is centered at the origin, the phase variables are continuous across the boundary between the two media. A continuous phase across boundaries is a requirement when specifying the phase.

For this simple geometry, it would also have been possible to specify the phase using wave vectors that are different for the two media. However, in more complex geometries, it is not possible to use this approach as the phase expressions in this case are not continuous across all boundaries.

Results and Discussion

First, the results are computed for s-polarization, where the polarization is orthogonal to the plane of incidence (out-of-plane polarization). As shown in Figure 2, there are both a refracted and a reflected beam. The incident beam and the reflected beam form an inference pattern. Thanks to the fine mesh used in the model, the interference pattern is resolved. Equation 2 is also used to verify that the reflectance is correct. It should be close to 14.8%.

Figure 2: The incident, transmitted (refracted) and reflected Gaussian beams for s-polarization (out-of-plane polarization).

Figure 3 shows the results for p-polarization (in-plane polarization). As expected, when the beam is incident at the Brewster angle, there is no reflected beam, but only a refracted (transmitted) beam.

Figure 3: The incident and transmitted Gaussian beams for p-polarization (in-plane polarization). For this polarization, with Brewster angle incidence, the reflected beam is gone.

Wave_Optics_Module/Optical_Scattering/brewster_interface

Modeling Instructions

From the menu, choose .

New

In the window, click

Model Wizard

In the window, click

In the tree, select .

Click .

Click

In the tree, select .

Click

Global Definitions

Parameters 1

The parameters for the model will be read from a file.

In the window, under click .

In the window for , locate the section.

Click

Browse to the model’s Application Libraries folder and double-click the file brewster_interface.txt.

Geometry 1

Define the geometry as a rectangle with a diagonal boundary.

Rectangle 1 (r1)

In the toolbar, click

In the window for , locate the section.

In the text field, type b.

In the text field, type a.

Locate the section. From the list, choose .

Polygon 1 (pol1)

In the toolbar, click

In the window for , locate the section.

In the table, enter the following settings:


x (m)	y (m)
-b/2	a/2
b/2	-a/2

Click

Click the

button in the toolbar.

Add Material

In the toolbar, click

to open the window.

The leftmost part consists of air and the rightmost part will be glass.

Go to the window.

In the tree, select .

Click in the window toolbar.

In the toolbar, click

to close the window.

Materials

Glass

In the window, under right-click and choose .

In the window for , type Glass in the text field.

Select Domain 2 only.

Click the

button in the toolbar.

Define the refractive index for glass, using the parameter n2.

Locate the section. In the table, enter the following settings:


Property	Variable	Value	Unit	Property group
Refractive index, real part	n_iso ; nii = n_iso, nij = 0	n2	1	Refractive index

Definitions

Set up expressions for the user-defined phases for the two waves, with different expressions in the two domains.

Variables 1

In the window, under right-click and choose .

In the window for , locate the section.

From the list, choose .

Select Domain 1 only.

Click the

button in the toolbar.

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
phi1	k1x_airx+k1y_airy		Phase in air, first wave
phi2	k2x_airx+k2y_airy		Phase in air, second wave

Variables 2

In the window, right-click and choose .

In the window for , locate the section.

From the list, choose .

Select Domain 2 only.

Locate the section. In the table, enter the following settings:


Name	Expression	Unit	Description
phi1	k1x_glassx+k1y_glassy		Phase in glass, first wave
phi2	k2x_glassx+k2y_glassy		Phase in glass, second wave

Electromagnetic Waves, Beam Envelopes (ewbe)

Now, use the phase variables to define the user-defined phases for the two waves.

In the window, under click .

In the window for , locate the section.

From the list, choose .

In the φ1 text field, type phi1.

In the φ2 text field, type phi2.

First, simulate the case for s-polarization, where the polarization is orthogonal to the plane of incidence.

Locate the section. From the list, choose .

On the leftmost boundary, a normally incident Gaussian beam is expected.

Matched Boundary Condition 1

In the toolbar, click

and choose .

Select Boundary 1 only.

In the window for , locate the section.

From the list, choose .

In the w0 text field, type w0.

Specify the Eg0 vector as


0	x
0	y
1[V/m]	z

On this boundary, only an incident field is expected, but there should not be any scattered field. Thus, provide that information, with the following setting, to avoid any potential spurious solutions.

Find the subsection. Select the check box.

On the rightmost boundary, a transmitted Gaussian beam, propagating at an angle to the boundary normal, is expected. Thus, add a Matched Boundary Condition feature that will absorb this transmitted Gaussian beam.

Matched Boundary Condition 2

In the toolbar, click

and choose .

Select Boundaries 4 and 5 only.

In the window for , locate the section.

From the list, choose .

When specifying the user-defined phase functions, you defined wave 1 to correspond to the transmitted wave. Thus, here specify that there should be no second wave incident at this boundary.

The reflected wave, propagating toward the bottom boundary, will also propagate at an angle to the normal to the bottom boundary. Thus, add a Matched Boundary Condition feature here, too, to absorb the reflected beam.

Matched Boundary Condition 3

In the toolbar, click

and choose .

Select Boundary 2 only.

Notice that when the user-defined phase functions were defined, the second wave was defined to correspond to the reflected wave. Thus, there should be no first wave incident at this boundary. Because this is the default setting, you do not need to make any manual settings.

Definitions

Set up integration operators to calculate the power of the incident, reflected, and transmitted beams.

Integration 1 (intop1)

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Select Boundary 1 only.

Integration 2 (intop2)

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Select Boundaries 4 and 5 only.

Integration 3 (intop3)

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Select Boundary 2 only.

Variables 3

Now, define the power variables for the beams, using the previously defined integration operators.

In the window, right-click and choose .

In the window for , locate the section.

In the table, enter the following settings:


Name	Expression	Unit	Description
Pin	-intop1(ewbe.nPoav)	W/m	Input power
Pt	intop2(ewbe.nPoav)	W/m	Transmitted power
Pr	intop3(ewbe.nPoav)	W/m	Reflected power

The minus sign for the input power is used as the power flow and the boundary normal point in the opposite directions.

Mesh 1

Let the physics define a triangular mesh where the maximum mesh element size is set to half a wavelength, to resolve the interference pattern created by the incident and the reflected beam.

In the window, under click .

In the window for , locate the section.

From the list, choose .

In the hmax text field, type lda0/2.

Study 1

Step 1: Frequency Domain

Define the frequency and compute the solution for the model.

In the window, under click .

In the window for , locate the section.

In the text field, type f0.

In the toolbar, click

Results

Electric Field

To really resolve the inference pattern to the left of the air-glass interface, set the resolution to extra fine.

In the window, expand the node, then click .

In the window for , click to expand the section.

From the list, choose .

In the toolbar, click

Click the

button in the toolbar. Compare your result with Figure 2.

Using the defined variables, compute the reflectance.

Global Evaluation 1

In the toolbar, click

In the window for , locate the section.

In the table, enter the following settings:


Expression	Unit	Description
Pr/Pin	1

Click

Table

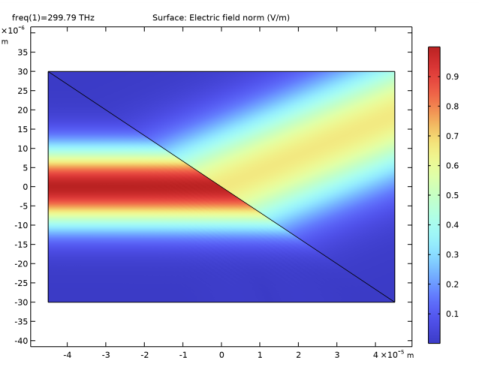
Go to the window. Compare the calculated reflectance with the theoretical value for s-polarized plane waves. Notice that the values are almost the same.