
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Stationary.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file curve_fit_mooney_rivlin.csv.
|
|
5
|
Locate the Column Settings section. In the table, click to select the cell at row number 1 and column number 2.
|
|
7
|
|
8
|
|
10
|
|
11
|
|
12
|
|
13
|
|
15
|
|
16
|
Find the Solver settings subsection. From the Least-squares time/parameter method list, choose From least-squares objective.
|
|
17
|
|
1
|
|
2
|
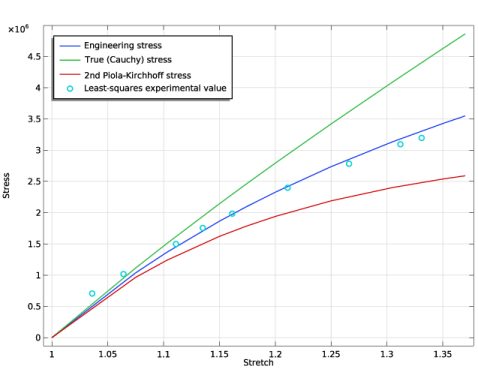
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Global definitions>Variables>P - Engineering stress - Pa.
|
|
3
|
|
1
|
|
2
|
In the Settings window for Global, click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Solver>Parameter estimation>opt.glsobj.engStress.data - Least-squares experimental value - Pa.
|
|
3
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Stretch.
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Solver>Control parameters>C10 - Mooney-Rivlin parameter - Pa.
|
|
3
|
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Solver>Control parameters>C01 - Mooney-Rivlin parameter - Pa.
|
|
4
|