
|
|
•
|
|
•
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Locate the Geometric Entity Selection section. From the Geometric entity level list, choose Boundary.
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Radiation in Participating Media (rpm).
|
|
2
|
In the Settings window for Radiation in Participating Media, locate the Participating Media Settings section.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the Radiation in Participating Media (rpm) node, then click Participating Medium 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Right-click Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1 and choose Fully Coupled.
|
|
6
|
Right-click Study 1>Solver Configurations>Solution 1 (sol1)>Stationary Solver 1>AMG, radiation variables and choose Enable.
|
|
7
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Net Radiative Heat Flux vs. z, 1D in the Label text field.
|
|
1
|
|
2
|
|
4
|
|
5
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Radiation in Participating Media>Boundary fluxes>rpm.qr_net - Net radiative heat flux - W/m².
|
|
6
|
Click Replace Expression in the upper-right corner of the x-Axis Data section. From the menu, choose Component 1 (comp1)>Geometry>Coordinate>z - z-coordinate.
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|
|
1
|
|
2
|
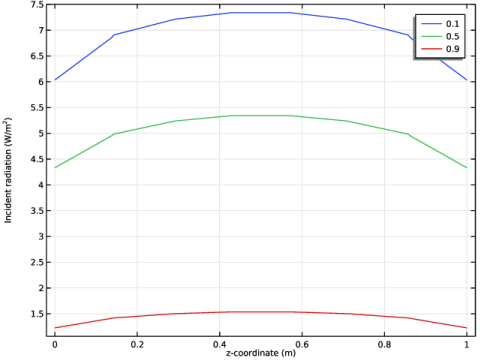
In the Settings window for 1D Plot Group, type Incident Radiation vs. z, 1D in the Label text field.
|
|
3
|
|
1
|
|
2
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the x-Axis Data section. From the menu, choose Component 1 (comp1)>Geometry>Coordinate>z - z-coordinate.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Incident Radiation vs. x, 1D in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Line Graph, click Replace Expression in the upper-right corner of the x-Axis Data section. From the menu, choose Component 1 (comp1)>Geometry>Coordinate>x - x-coordinate.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
5
|
Locate the Surface Radiative Properties section. From the ε list, choose User defined. In the associated text field, type ew*(1-y/R).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
In the Model Builder window, expand the Study 2>Solver Configurations>Solution 2 (sol2) node, then click Dependent Variables 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Incident Radiation vs. Azimuthal Angle, 1D in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Azimuthal angle (rad).
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Radiation in Participating Media (rpm) click Participating Medium 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
In the Model Builder window, expand the Study 3>Solver Configurations>Solution 3 (sol3) node, then click Dependent Variables 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
In the Model Builder window, expand the Study 3>Solver Configurations>Solution 3 (sol3)>Stationary Solver 1 node.
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
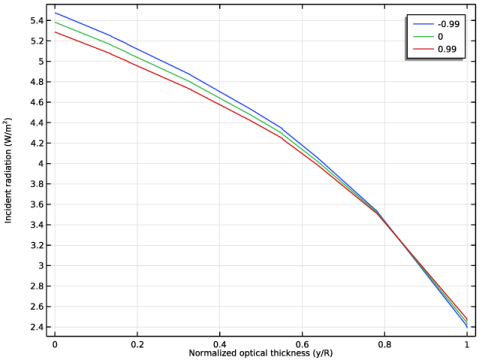
In the Settings window for 1D Plot Group, type Incident Radiation vs. Normalized Optical Thickness, 1D in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Normalized optical thickness (y/R).
|
|
6
|
|
7
|