
|
|
1
|
|
2
|
In the Select Physics tree, select Fluid Flow>Shallow Water Equations>Shallow Water Equations, Time Explicit (swe).
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
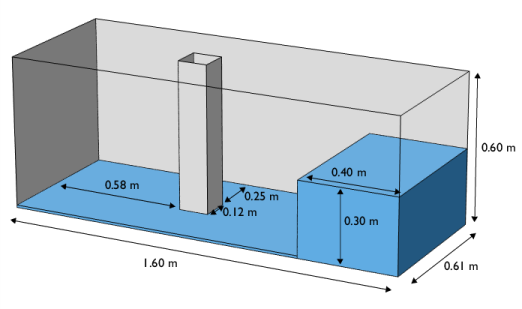
Select the object r1 only.
|
|
3
|
|
4
|
|
5
|
Select the object sq1 only.
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Shallow Water Equations, Time Explicit (swe) click Initial Values 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
7
|
|
8
|
Select the Description check box.
|
|
9
|
In the associated text field, type Pressure force on the column.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
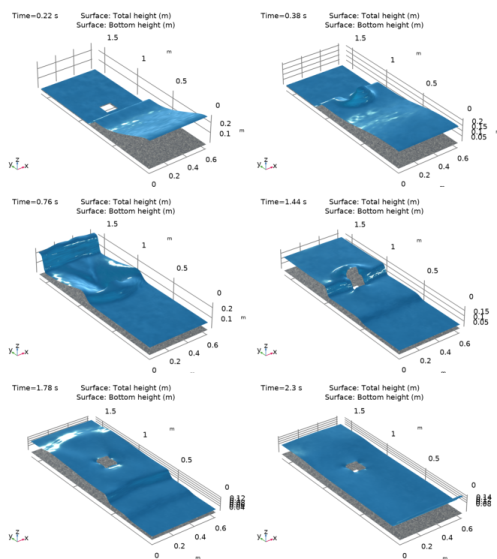
In the Model Builder window, expand the Results>Total Height (swe)>Total Height node, then click Height Expression 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|