PDF
Parameter Estimation of a Time-Dependent Lumped Battery Model
Introduction
This tutorial uses a “black-box” approach to define a battery model based on a small set of lumped parameters, requiring no knowledge of the internal structure or design of the battery electrodes, or choice of materials. The inputs to the model are the battery capacity, the initial state-of-charge (SOC), and an open circuit voltage versus SOC curve, in combination with load cycle experimental data.
Parameter estimation of the lumped parameters is achieved using the Parameter Estimation study step.
Model Definition
The model could be seen as a lumped version of a single particle model, modeling the transport of intercalated lithium in one of the electrodes. This simplification can be motivated as long as the battery is mainly governed by the diffusion process in one of the electrodes only. The single particle modeling approach is exemplified in the Application Library example Single Particle Model of a Lithium-Ion Battery.
This model uses the Lumped Battery interface and calculates the battery cell voltage Ecell (V) subject to an applied time-dependent cell current Icell (A). The parameters used in the model are described in Table 1. Additionally, the model requires the battery open circuit voltage data, EOCV (V), as function of state-of-charge.
Table 1: Model parameters.
Parameter
Unit
Description
 Qcell,0
A·h
Battery capacity
 SOC0
1
Initial state-of-charge
 ηIR, 1C
V
Ohmic overpotential at 1C
 J0
1
Dimensionless charge exchange current
 τ
s
Diffusion time constant
Potential losses due to ohmic and Charge Transfer processes
The lumped voltage loss associated with ohmic process in the electrolyte and electrodes is given as,
where ηIR,1C (V) is the ohmic overpotential at 1C, Icell is the applied current, and the 1C current, I1C (A), is defined as,
where Qcell,0 (C) is the battery cell capacity.
The dimensionless charge exchange current J0 is used to define the lumped voltage loss associated with the charge transfer reactions (activation overpotential) on both the positive and negative electrode surfaces as
where R denotes the molar gas constant, T the temperature, and F Faraday’s constant.
Potential Loss due to diffusion processes
Concentration overpotential effects can be accounted for in the Lumped Battery interface either based on diffusion in an idealized particle or by using an RC pair (a linear resistor coupled in parallel with a capacitor). In this model, particle diffusion is considered. In this case, Fickian diffusion of a dimensionless SOC variable is solved for in a 1D pseudo extra dimension corresponding to the particle dimension of length 1 with X as the dimensionless spatial variable, using spherical symmetry (for spherical particles), according to
where τ (s) is the diffusion time constant. The interval represents an average particle of the electrode governing the battery, where X = 0 and X = 1 represent the center and surface of the particle, respectively.
The boundary conditions at the center and surface of the particle are as follows:
where Nshape is 3 for spherical particles. The initial cell state-of-charge is specified by SOC0. The surface state-of-charge, SOCsurface, is defined at the surface of the particle (X = 1). The average state-of-charge, SOCaverage, is defined by integrating over the volume of the particle, appropriately considering spherical coordinates, and is defined as
(1)
The lumped voltage loss associated with concentration overpotential is defined as,
Cell potential and Parameter Estimation
Finally, the battery cell voltage Ecell is defined as
Introducing the expression for ηconc, Ecell can also be defined as
The tutorial consists of three parts. In the first part, a lumped battery model (of capacity 12 Ah) is set up and run for a time-dependent battery current. In the second part, parameter estimation of the parameters ηIR, 1C, τ, and J0, is performed using experimental data. This is done using a Parameter Estimation study step using a Levenberg–Marquardt optimization solver. Note, the second part of the tutorial requires the Optimization module. In the third part, cell voltage prediction is performed using the optimized lumped parameter values that were obtained in the previous parameter estimation study, and compared with experimental data. The first two studies use a 300 s load cycle. The third prediction study uses a full load cycle with additional 300 s.
Results and Discussion
Figure 1 shows the modeled cell voltage using the fitted parameter values from Table 2 together with the experimental cell voltage and the corresponding open circuit voltage, for the 300 s load cycle.
Figure 1: Modeled cell voltage using the fitted parameter values, experimental cell voltage, and corresponding open circuit voltage, for the 300 s load cycle.
 
Table 2: Fitted parameter values.
Parameter
Value
Unit
 ηIR, 1C
4.5
mV
 J0
1.16
1
 τ
1375
s
Figure 2 shows the ohmic, activation and concentration related voltage losses for the 300 s load cycle using the fitted parameter values.
Figure 2: Ohmic, charge transfer and concentration voltage losses using the fitted parameter values, for the 300 s load cycle. Corresponding cell current load shown on second y-axis.
Figure 3 shows the predicted cell voltage using the optimized parameter values from Table 2 together with the experimental cell voltage and the corresponding open circuit voltage, for the full 600 s load cycle. (Note that the first half (300 s) of the predicted cell voltage is exactly similar to Figure 1, as expected).
Figure 3: Predicted cell voltage using the optimized parameter values, experimental cell voltage, and corresponding open circuit voltage, for the full 600 s load cycle.
 
Table 3: Standard deviation: Cell voltage.
Study
Standard deviation
Load curve simulation
 0.031
Parameter estimation
 0.015
Full load curve prediction
 0.014
The standard deviation values of the modeled cell voltage from the experimental values for all the three studies is shown in Table 3. The standard deviation value of first Load curve simulation study is high, as expected, considering that default values of the lumped parameters are used to simulate the cell voltage. The standard deviation value of the second Parameter estimation study and the third Full load curve prediction study are much lower and nearly the same. (Note that the standard deviation calculation of the prediction study uses only the latter half of the full load cycle). The nearly identical standard deviation values of the second and third study indicate that the quality of prediction will be only as good as the quality of parameter estimation and optimization.
Notes About the COMSOL Implementation
In the model, the inverse of J0, invJ0, is used as fitting parameter. This is done in order to avoid division by 0 in the activation overpotential expression during the optimization process.
Reference
1. H. Ekström, B. Fridholm, and G. Lindbergh, “Comparison of lumped diffusion models for voltage prediction of a lithium-ion battery cell during dynamic loads,” J. Power Sources, vol. 402, pp. 296–300, 2018.
Application Library path: Battery_Design_Module/Batteries,_Lithium-Ion/lumped_li_battery_parameter_estimation
Modeling Instructions
This tutorial consists of three parts. In the first part you will learn how to build a lumped battery model and run a simulation for a time-dependent battery current. In the second part you will perform parameter estimation using experimental data. The second part of the tutorial requires the Optimization Module. In the third part, you will perform a prediction study using the optimized lumped parameter values that were obtained in the previous parameter estimation study, and compare with experimental data.
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  0D.
2
In the Select Physics tree, select Electrochemistry>Batteries>Lumped Battery (lb).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Time Dependent.
6
Click  Done.
Global Definitions
Parameters 1
Import the model parameters from a text file.
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file lumped_li_battery_parameter_estimation_parameters.txt.
Definitions
The battery current and the experimental cell voltage are time-dependent. Therefore you need to define these as variables. (The experimental cell voltage variable will only be used during postprocessing.)
Variables 1
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
2
In the Settings window for Variables, locate the Variables section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file lumped_li_battery_parameter_estimation_variables.txt.
The expressions in the variable list are marked in orange, indicating unknown operators and functions. You will now proceed to add the missing interpolation function for the cell voltage and current versus time.
Results
We will import the battery load and experimental cell voltage data as a table, and use this table both for defining time-dependent battery current and experimental voltage functions, as well as for the objective function used in the second part of the tutorial.
Load Cycle Data
1
In the Model Builder window, expand the Results node.
2
Right-click Results>Tables and choose Table.
3
In the Settings window for Table, type Load Cycle Data in the Label text field.
4
Locate the Data section. Click Import.
5
Browse to the model’s Application Libraries folder and double-click the file lumped_li_battery_parameter_estimation_E_I_vs_t_data.txt.
Table
1
Go to the Table window.
The data file contains three different columns: Time, Current and Voltage.
Definitions
Interpolation - E and I vs. t
1
In the Home toolbar, click  Functions and choose Global>Interpolation.
2
In the Settings window for Interpolation, type Interpolation - E and I vs. t in the Label text field.
3
Locate the Definition section. From the Data source list, choose Result table.
(Note that, instead of using the table, you could have imported the data file directly here too.)
4
Find the Functions subsection. In the table, enter the following settings:
Function name
Position in file
E_cell_exp
1
I_cell_exp
2
5
Locate the Units section. In the Argument table, enter the following settings:
Argument
Unit
Column 1
s
Lumped Battery (lb)
You will now start defining the battery model.
1
In the Model Builder window, under Component 1 (comp1) click Lumped Battery (lb).
2
In the Settings window for Lumped Battery, locate the Operation Mode section.
3
In the Iapp text field, type I_cell_exp.
4
Locate the Battery Settings section. In the Qcell,0 text field, type Q_cell0.
5
In the SOCcell,0 text field, type SOC_0.
Q_cell0 and SOC_0 were defined in the parameter text file you imported before.
(The Battery volume parameter is only used to calculate the heat source, in the unit W/m3, and is not needed in this model.)
Cell Equilibrium Potential 1
Load the open circuit voltage data at the reference temperature from a text file. Note that in this model the reference temperature is same as the simulation temperature.
1
In the Model Builder window, under Component 1 (comp1)>Lumped Battery (lb) click Cell Equilibrium Potential 1.
2
In the Settings window for Cell Equilibrium Potential, locate the Open Circuit Voltage section.
3
Click  Clear Table.
Note that it is important to clear the table before loading data from the text file.
4
Click  Load from File.
5
Browse to the model’s Application Libraries folder and double-click the file lumped_li_battery_parameter_estimation_E_OCP_data.txt.
6
In the Tref text field, type T.
Note that in this node you may also add data for the temperature derivative of open circuit voltage, that is used to calculate the temperature dependence of the open circuit voltage. Additionally, this data is used in the calculation of the reversible (entropic) contribution and heat of mixing contribution to the total heat source. However, this data is not needed in this model.
Voltage Losses 1
Keep the default values for the Voltage Losses parameters for now, but enable also the concentration overpotential.
1
In the Model Builder window, click Voltage Losses 1.
2
In the Settings window for Voltage Losses, locate the Concentration Overpotential section.
3
Select the Include concentration overpotential check box.
Study 1 - Load Curve Simulation
The battery model is now ready for solving.
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, type Study 1 - Load Curve Simulation in the Label text field.
Step 1: Time Dependent
1
In the Model Builder window, under Study 1 - Load Curve Simulation click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
In the Output times text field, type range(0,1,300).
The above setting tells the solver to run a simulation for 300 s and store the solution every second.
4
From the Tolerance list, choose User controlled.
5
In the Relative tolerance text field, type 0.001.
6
In the Home toolbar, click  Compute.
Results
Cell Voltage
A number of plots were created by default. You will now modify the first plot to compare the modeled cell voltage with the experimental data.
1
In the Settings window for 1D Plot Group, type Cell Voltage in the Label text field.
2
Click to expand the Title section. From the Title type list, choose None.
3
Locate the Plot Settings section. Clear the Two y-axes check box.
4
Locate the Legend section. From the Position list, choose Lower right.
Global 1
1
In the Model Builder window, expand the Cell Voltage node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
lb.E_cell
V
Modeled cell voltage
Global 3
1
In the Model Builder window, click Global 3.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Definitions>Variables>E_cell_exp - Experimental cell voltage - V.
Cell Voltage
1
In the Model Builder window, click Cell Voltage.
2
In the Settings window for 1D Plot Group, locate the Axis section.
3
Select the Manual axis limits check box.
4
In the x maximum text field, type 305.
5
In the y minimum text field, type 3.35.
6
In the y maximum text field, type 4.2.
7
In the Cell Voltage toolbar, click  Plot.
Cell State-of-Charge (lb)
Also a state-of-charge versus time plot was created by default:
Voltage Losses and Load
Proceed as follows to create a plot that compares the different voltage losses in the model:
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Voltage Losses and Load in the Label text field.
Global 1
1
Right-click Voltage Losses and Load and choose Global.
2
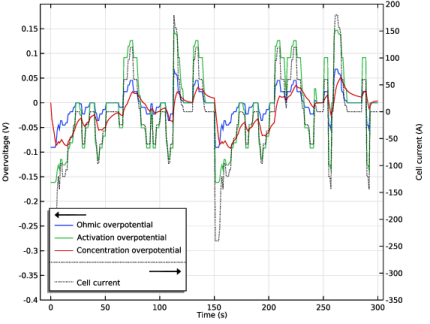
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lumped Battery>Overpotentials>lb.eta_ir - Ohmic overpotential - V.
3
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lumped Battery>Overpotentials>lb.eta_act - Activation overpotential - V.
4
Click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lumped Battery>Overpotentials>lb.eta_conc - Concentration overpotential - V.
5
Locate the x-Axis Data section. From the Parameter list, choose Expression.
6
In the Expression text field, type t.
Global 2
1
In the Model Builder window, right-click Voltage Losses and Load and choose Global.
2
In the Settings window for Global, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Lumped Battery>lb.I_cell - Cell current - A.
3
Locate the x-Axis Data section. From the Parameter list, choose Expression.
4
In the Expression text field, type t.
5
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dotted.
6
From the Color list, choose Black.
Voltage Losses and Load
1
In the Model Builder window, click Voltage Losses and Load.
2
In the Settings window for 1D Plot Group, locate the Title section.
3
From the Title type list, choose None.
4
Locate the Plot Settings section. Select the y-axis label check box.
5
In the associated text field, type Overvoltage (V).
6
Select the Two y-axes check box.
7
In the table, select the Plot on secondary y-axis check box for Global 2.
8
Locate the Axis section. Select the Manual axis limits check box.
9
In the x maximum text field, type 305.
10
In the y minimum text field, type -0.4.
11
In the y maximum text field, type 0.2.
12
In the Secondary y minimum text field, type -350.
13
In the Secondary y maximum text field, type 200.
14
Locate the Legend section. From the Position list, choose Lower left.
15
In the Voltage Losses and Load toolbar, click  Plot.
Lumped Battery (lb)
Voltage Losses 1
1
In the Model Builder window, under Component 1 (comp1)>Lumped Battery (lb) click Voltage Losses 1.
2
In the Settings window for Voltage Losses, locate the Model Input section.
3
In the T text field, type T.
Now change the default values for the voltage losses to use values defined in the Parameters node instead.
4
Locate the Ohmic Overpotential section. In the ηIR,1C text field, type eta_IR_1C.
5
Locate the Activation Overpotential section. In the J0 text field, type J0.
6
Locate the Concentration Overpotential section. In the τ text field, type tau.
Root
The next step is to set up the optimization solver used for the parameter estimation. We will do this in a new study node.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2 - Parameter Estimation
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, type Study 2 - Parameter Estimation in the Label text field.
3
Locate the Study Settings section. Clear the Generate default plots check box.
The first part of the tutorial is now complete. In the second part you will learn how to run an optimization solver to perform an estimation of the different voltage loss parameters. For the second part you need an Optimization Module license.
Parameter Estimation
1
In the Study toolbar, click  Optimization and choose Parameter Estimation.
The Parameter Estimation study step is used to construct the objective function that is to be minimized by the optimization solver. The objective function in this case will equal the sum of the squared differences between the modeled and the experimental cell voltages, for all stored times in the data.
2
In the Settings window for Parameter Estimation, locate the Experimental Data section.
3
From the Data source list, choose Result table.
Note that you can also import a data file directly here instead of using the table.
4
Locate the Column Settings section. In the table, click to select the cell at row number 2 and column number 3.
5
In the table, enter the following settings:
Columns
Type
Settings
Time (s)
Time
Time unit=s
Voltage (V)
Value
Model expression=comp1.lb.E_cell, Name=col2, Weight=1
Current (A)
Ignored column
 
6
In the Model expression text field, type comp1.lb.E_cell.
The Model expression tells what value in the model the data corresponds to.
7
In the Unit text field, type V.
Now define what parameters (control variables) we should run the parameter estimation for:
8
Locate the Parameters section. Click  Add three times.
There should now be three control variables present in the table. In order to improve the optimization you need to provide suitable scales for these (the Scale column in the table).
9
In the table, enter the following settings:
Parameter name
Initial value
Scale
Lower bound
Upper bound
eta_IR_1C (Ohmic overpotential at 1C, fitting parameter)
10[mV]
0.01
 
 
invJ0 (Inverse dimensionless charge exchange current, fitting parameter)
1
1
 
 
tau (Diffusion time constant, fitting parameter)
1000[s]
1000
 
 
(The Lower/Upper bound columns are not supported by the Levenberg-Marquardt solver, but other solver (such as SNOPT) allow you to put bounds on the control variables during the optimization.)
The Levenberg-Marquardt is suitable for global least-squares problems.
10
Locate the Parameter Estimation Method section. From the Method list, choose Levenberg-Marquardt.
11
Find the Solver settings subsection. From the Least-squares time/parameter method list, choose From least-squares objective.
Definitions (comp1)
Global Variable Probe 1 (var1)
By adding probes for the fitting parameters (the control variables) you can monitor how these change during the optimization.
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Global Variable Probe.
2
In the Settings window for Global Variable Probe, locate the Expression section.
3
In the Expression text field, type eta_IR_1C.
Global Variable Probe 2 (var2)
1
Right-click Definitions and choose Global Variable Probe.
2
In the Settings window for Global Variable Probe, locate the Expression section.
3
In the Expression text field, type invJ0.
Global Variable Probe 3 (var3)
1
Right-click Definitions and choose Global Variable Probe.
2
In the Settings window for Global Variable Probe, locate the Expression section.
3
In the Expression text field, type tau.
Study 2 - Parameter Estimation
The parameter estimation problem is now ready for solving. Since the model will run multiple times in order to find the minimum of the objective function, this computation will take a little longer (about a minute) to run than the first study.
1
In the Study toolbar, click  Compute.
Results
Change what data the plots are pointing to in order to plot the results of the parameter estimation study (Figure 1 and Figure 2).
Cell Voltage
1
In the Model Builder window, under Results click Cell Voltage.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 2 - Parameter Estimation/Solution 2 (sol2).
4
In the Cell Voltage toolbar, click  Plot.
Voltage Losses and Load
1
In the Model Builder window, click Voltage Losses and Load.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 2 - Parameter Estimation/Solution 2 (sol2).
4
In the Voltage Losses and Load toolbar, click  Plot.
Study 2 - Parameter Estimation
The cell voltage plot can be set as output while solving to monitor the optimization process in the graphics window during computation.
Parameter Estimation
1
In the Model Builder window, under Study 2 - Parameter Estimation click Parameter Estimation.
2
In the Settings window for Parameter Estimation, click to expand the Output While Solving section.
3
Select the Plot check box.
You may now try to recompute the solution to see how the experimental and model cell voltage curves approach each other during optimization.
Results
The second part of the tutorial is now complete. The final part is to set up a new study for cell voltage prediction. Note that the previous two studies used a 300 s load cycle data. For the prediction study, a full load cycle with additional 300 s will be used. First, we will import the full load cycle data consisting of the battery load and experimental cell voltage data as a table, as before, and use this table for defining time-dependent battery current and experimental voltage functions. (Note that the initial 300 s of the full load cycle data is exactly identical to the load cycle data imported for the previous study).
Full Load Cycle Data
1
In the Results toolbar, click  Table.
2
In the Settings window for Table, type Full Load Cycle Data in the Label text field.
3
Locate the Data section. Click Import.
4
Browse to the model’s Application Libraries folder and double-click the file lumped_li_battery_parameter_estimation_E_I_vs_t_fulldata.txt.
Table
1
Go to the Table window.
This data file also contains three different columns: Time, Current and Voltage, as before.
Definitions (comp1)
Interpolation - E and I vs. t (full)
1
In the Home toolbar, click  Functions and choose Global>Interpolation.
2
In the Settings window for Interpolation, type Interpolation - E and I vs. t (full) in the Label text field.
3
Locate the Definition section. From the Data source list, choose Result table.
4
From the Table from list, choose Full Load Cycle Data.
5
Find the Functions subsection. In the table, enter the following settings:
Function name
Position in file
E_cell_exp_full
1
I_cell_exp_full
2
6
Locate the Units section. In the Argument table, enter the following settings:
Argument
Unit
Column 1
s
Variables 1
Next, we will define variables corresponding to the time-dependent battery current and the experimental cell voltage of the full load cycle. (The experimental cell voltage variable will only be used during postprocessing.)
Variables 2
1
In the Model Builder window, under Component 1 (comp1)>Definitions right-click Variables 1 and choose Duplicate.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
I_cell_exp
I_cell_exp_full(t)[A]
A
Experimental cell current - full load cycle
E_cell_exp
E_cell_exp_full(t)[V]
V
Experimental cell voltage - full load cycle
Root
Add a new time-dependent study for prediction of the full 600 s load cycle. Modify the model configuration for this study step to disable Variables1 (that consists of variables corresponding to the 300 s load cycle) and the Optimization physics interface. Also, set up the study to use the optimized lumped parameter values from the previous parameter estimation study.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Time Dependent.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 3 - Full Load Curve Prediction
1
In the Model Builder window, click Study 3.
2
In the Settings window for Study, type Study 3 - Full Load Curve Prediction in the Label text field.
Step 1: Time Dependent
1
In the Model Builder window, under Study 3 - Full Load Curve Prediction click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
In the Output times text field, type range(0,1,600).
4
From the Tolerance list, choose User controlled.
5
In the Relative tolerance text field, type 0.001.
6
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
7
In the tree, select Component 1 (Comp1)>Definitions>Variables 1.
8
Click  Disable.
9
Click to expand the Values of Dependent Variables section. Find the Initial values of variables solved for subsection. From the Settings list, choose User controlled.
10
Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
11
From the Method list, choose Solution.
12
From the Study list, choose Study 2 - Parameter Estimation, Time Dependent.
13
In the Model Builder window, click Study 3 - Full Load Curve Prediction.
14
In the Settings window for Study, locate the Study Settings section.
15
Clear the Generate default plots check box.
Before we compute the prediction study, it may be useful, for completeness, to update the model configuration for the previous two study steps to disable Variables2 (that consists of variables corresponding to the 600 s full load cycle). Also disable the Optimization physics interface in the first study.
Study 1 - Load Curve Simulation
Step 1: Time Dependent
1
In the Model Builder window, under Study 1 - Load Curve Simulation click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (Comp1)>Definitions>Variables 2.
5
Click  Disable.
Study 2 - Parameter Estimation
Step 1: Time Dependent
1
In the Model Builder window, under Study 2 - Parameter Estimation click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (Comp1)>Definitions>Variables 2.
5
Click  Disable.
Study 3 - Full Load Curve Prediction
In the Home toolbar, click  Compute.
Results
The results of the prediction study (Figure 3) can be plotted by duplicating the Cell Voltage figure.
Cell Voltage: Full Cycle Prediction
1
In the Model Builder window, right-click Cell Voltage and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Cell Voltage: Full Cycle Prediction in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 3 - Full Load Curve Prediction/Solution 3 (sol3).
4
Locate the Axis section. In the x maximum text field, type 610.
5
Locate the Legend section. From the Position list, choose Lower left.
Global 1
1
In the Model Builder window, expand the Cell Voltage: Full Cycle Prediction node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
lb.E_cell
V
Predicted cell voltage
4
In the Cell Voltage: Full Cycle Prediction toolbar, click  Plot.
Global Evaluation: Standard Deviation (Study1)
Finally, you can set up global evaluations for calculating the standard deviation of the modeled cell voltage from the experimental values for all the three studies as follows:
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Global Evaluation: Standard Deviation (Study1) in the Label text field.
3
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
lb.E_cell-E_cell_exp
V
 
4
Locate the Data Series Operation section. From the Transformation list, choose Standard deviation.
5
Click  Evaluate.
Global Evaluation: Standard Deviation (Study2)
1
Right-click Global Evaluation: Standard Deviation (Study1) and choose Duplicate.
2
In the Settings window for Global Evaluation, type Global Evaluation: Standard Deviation (Study2) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 2 - Parameter Estimation/Solution 2 (sol2).
4
Click  Evaluate.
Global Evaluation: Standard Deviation (Study3)
1
Right-click Global Evaluation: Standard Deviation (Study2) and choose Duplicate.
2
In the Settings window for Global Evaluation, type Global Evaluation: Standard Deviation (Study3) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 3 - Full Load Curve Prediction/Solution 3 (sol3).
You can choose only the latter half of the full load cycle to obtain the standard deviation of the prediction study.
4
From the Time selection list, choose Manual.
5
In the Time indices (1-601) text field, type range(302,1,601).
6
Click  Evaluate.