Theory for the Wall Boundary Condition

See Wall for the node settings.

The Slip condition assumes that there are no viscous effects at the slip wall and hence, no boundary layer develops. From a modeling point of view, this is a reasonable approximation if the important effect of the wall is to prevent fluid from leaving the domain. Mathematically, the constraint can be formulated as:

The no-penetration term takes precedence over the Neumann part of the condition and the above expression is therefore equivalent to

expressing that there is no flow across the boundary and no viscous stress in the tangential direction.

For a moving wall with translational velocity utr, u in the above equations is replaced by the relative velocity urel = u−utr.

The boundary condition for ν is

Porous slip

The option, which can be chosen in the list when is activated, results in special treatment of boundaries and boundaries adjacent to porous domains ( feature). Namely, similar to the boundary condition, no penetration and tangential stress conditions are applied at the wall:

Here,

is the viscous wall traction,

is the wall normal,

is the tangential velocity at the wall while the real no slip is assumed to be at a distance

(half-height of the first cell adjacent to the wall) outside the wall, and

is the porous slip length. An analytical derivation of the velocity profile in the boundary layer where the pressure gradient is balanced by the sum of the Darcy term, Forchheimer drag, and a viscous term (neglecting convective terms) leads to the following expression for

where

is the porous length scale,

is the non-Darcian coefficient (

is the Forchheimer coefficient),

is the gravity vector, and

are intermediate variables. This formula is used when the is chosen and it reads pressure-gradient at the wall. By default, the is activated and the corresponding formula is:

Although this formulation is an approximation, since it uses slip velocity at the wall to reconstruct the pressure gradient, it is rather accurate. Moreover, the influence of convective terms is partially accounted for in this formulation.

Sliding Wall

The sliding wall option is appropriate if the wall behaves like a conveyor belt; that is, the surface is sliding in its tangential direction. The wall does not have to actually move in the coordinate system.

•

In 2D, the tangential direction is unambiguously defined by the direction of the boundary, but the situation becomes more complicated in 3D. For this reason, this boundary condition has slightly different definitions in the different space dimensions.

•

For 2D and 2D axisymmetric components, the velocity is given as a scalar Uw and the condition prescribes

where t = (ny , −nx) for 2D and t = (nz, −nr) for axial symmetry.

•

For 3D components, the velocity is set equal to a given vector uw projected onto the boundary plane:

The normalization makes u have the same magnitude as uw even if uw is not exactly parallel to the wall.

Slip Velocity

In the microscale range, the flow at a boundary is seldom strictly no slip or slip. Instead, the boundary condition is something in between, and there is a slip velocity at the boundary. Two phenomena account for this velocity: violation of the continuum hypothesis for the viscosity and flow induced by a thermal gradient along the boundary.

The following equation relates the viscosity-induced jump in tangential velocity to the tangential shear stress along the boundary:

For gaseous fluids, the coefficient β is given by

where μ is the fluid’s dynamic viscosity (SI unit: Pa·s), αv represents the tangential momentum accommodation coefficient (TMAC) (dimensionless), and λ is the molecules’ mean free path (SI unit: m). The tangential accommodation coefficients are typically in the range of 0.85 to 1.0 and can be found in Ref. 17.

A simpler expression for β is

where Ls, the slip length (SI unit: m), is a straight channel measure of the distance from the boundary to the virtual point outside the flow domain where the flow profile extrapolates to zero. This equation holds for both liquids and gases.

Thermal creep results from a temperature gradient along the boundary. The following equation relates the thermally-induced jump in tangential velocity to the tangential gradient of the natural logarithm of the temperature along the boundary:

where σT is the thermal slip coefficient (dimensionless) and ρ is the density of the fluid. The thermal slip coefficients range between 0.3 and 1.0 and can be found in Ref. 17.

Combining the previous relationships results in the following equation:

Relate the tangential shear stress to the viscous boundary force by

where the components of K are the Lagrange multipliers that are used to implement the boundary condition. Similarly, the tangential temperature gradient results from the difference of the gradient and its normal projection:

Use Viscous Slip

When viscous slip is used, select Maxwell’s model to calculate Ls using:

Also see Wall for the node settings.

Electroosmotic Velocity

Most solid surfaces acquire a surface charge when brought into contact with an electrolyte. In response to the spontaneously formed surface charge, a charged solution forms close to the liquid-solid interface. This is known as an electric double layer. If an electric field is applied to the fluid, this very narrow layer starts to move along the boundary.

It is possible to model the fluid’s velocity near the boundary using the Helmholtz-Smoluchowski relationship between the electroosmotic velocity u and the applied electric field:

where μeo is the electroosmotic mobility and Et is the fluid electric field tangential to the wall.

Built-in Expression

Use the Electroosmotic mobility μeo (SI unit: m2/(s·V)) Built-in expression to compute the electroosmotic mobility from:

(3-22)

Here εr is the fluid’s relative permittivity, ε0 the permittivity of free space (SI unit F/m), which is a predefined physical constant, ζ is the fluid’s zeta potential (SI unit: V), and μ the fluid’s dynamic viscosity (Pa·s). Typically μeo≈7×10-8m2/(s·V) and ζ≈100 mV (see H. Bruus, Theoretical Microfluidics, Oxford University Press, 2008). See Wall for the node settings.


	Electroosmotic Micromixer: Application Library path Microfluidics_Module/Micromixers/electroosmotic_mixer

Navier Slip

This boundary condition enforces no-penetration at the wall,

, and adds a tangential stress

where

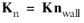and K is the viscous stress tensor. β is a slip length, and

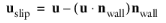
is the velocity tangential to the wall. The boundary condition does not set the tangential velocity component to zero; however, the extrapolated tangential velocity component is 0 at a distance β outside the wall.

The setting is per default set to . The slip length β is then defined as

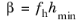
, where

is the smallest element side (corresponds to the element size in the wall normal direction for boundary layer elements) and

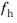
is a user input.

In cases where the wall movement is nonzero, may be selected to use

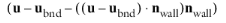
instead of

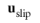
in the friction force. Then, the extrapolated tangential velocity component is

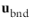
at a distance β outside of the wall. Note that the uw is always accounted for in the friction force.

The Navier Slip boundary condition is suitable for walls adjacent to a fluid-fluid interface or a free surface when solving for laminar flow. Applying this boundary condition, the contact line (fluid-fluid-solid interface) is free to move along the wall. Note that in problems with contact lines, the tangential velocity of the wall typically represents the movement of the contact line but the physical wall is not moving. In such cases, should not be checked.

The Navier Slip option is not available when selecting a turbulence model.

Constraint Settings

The wall feature uses three different techniques to constraint the velocity field:

•

Pointwise constraints is the standard technique to enforce strong constraints in the finite element method. The desired value of the velocity is prescribed at each node point in the mesh. Since the constraint is enforced locally at each node, only local values are affected by the constraint and the constraints are independent of each other. The solvers can therefore eliminate both the constrained degrees of freedom and the constraint force terms, effectively reducing the number of degrees of freedom being solved for.

The main advantage of pointwise constraints is that they enforce the constraint exactly pointwise. This means that they do not introduce any leakage of the velocity across the wall, unless specified. The main disadvantage of pointwise constraints is that they introduce locking effects when trying to impose a no-penetration condition for the velocity, u · n = 0, on curved walls or walls with sharp corners.

•

Using Weak constraints is an alternative method to prescribe the velocity. It consists on enforcing the boundary condition for the velocity via Lagrange multipliers. Their main advantage is that the Lagrange multiplier can provide an accurate representation of the reaction flux at the wall. Their main disadvantage is that they introduce extra unknowns, and are usually difficult to combine with other constraint methods on adjacent boundaries. Moreover, they may require extra constraints for the Lagrange multipliers. For more information, see Weak Constraints in the COMSOL Multiphysics Reference Manual.

•

Discontinuous Galerkin (DG) constraints use a numerical flux to prescribe the velocity at the wall. They impose the constraint in a integral sense rather than pointwise, and do not suffer from the locking effects introduced by pointwise constraints when trying to prescribe a no penetration condition for the velocity. They are also better behaved when prescribing nonlinear constraints. Their main disadvantage is that the constraint is only imposed approximately, and may produce small leaks. For more information, see Discontinuous Galerkin Formulation.

The following combination of Constraint techniques can be selected in the Constraint Setting sections of Wall boundary conditions:

•

Use default settings. The default settings use different constraint methods depending on whether only the normal component of the velocity is prescribed, such as in the no penetration condition, u · n = 0, imposed for example in Slip walls or No Slip walls using Wall Functions or Automatic Wall Treatment, or both tangential and normal components are prescribed, as is the case of No Slip walls in laminar flow.

DG constraints are used to impose the no penetration condition for Slip walls. When a No Slip condition is prescribed, pointwise constraints are used except for moving walls where DG constraints are used.

•

Use Pointwise constraints.

•

Use DG constraints.

•

Use Weak constraints. Weak constraints are not available on Interior Walls.

•

Use Mixed constraints. This option is only available when both the tangential and normal components of the velocity need to be prescribed. The velocity on the wall normal direction is imposed via pointwise constraints. The constraint for the tangential directions is relaxed, and DG constraints are used instead. This provides improved accuracy and performance when working with coarse boundary layer meshes. For more information, see Ref. 19.