Linear Elastic Material

For a linear elastic material, Hooke’s law relates the stress tensor to the elastic strain tensor:

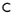is the 4th order elasticity tensor, “:” stands for the double-dot tensor product (or double contraction). The elastic strain εel is the difference between the total strain ε and all inelastic strains εinel. There may also be an extra stress contribution σex with contributions from initial stresses and viscoelastic stresses. In case of geometric nonlinearity, the second Piola–Kirchhoff stress tensor and the Green–Lagrange strain tensor are used.

The elastic strain energy density is

This expression assumes that the initial stress contribution is constant during the straining of the material.

Because of the symmetry, the strain tensor can be written as the following matrix:

Due to the symmetry, the elasticity tensor can be completely represented by a symmetric 6-by-6 matrix as:

which is the elasticity matrix.

In this case, the elasticity matrix becomes

Different pairs of elastic moduli can be used, and as long as two moduli are defined, the others can be computed according to Table 3-1.

Table 3-1: Expressions for the Elastic Moduli.
Description	Variable	D(E,ν)	D(E,G)	D(K,G)	D(λ,μ)
Young’s modulus	E =	E	E
Poisson’s ratio	ν =	ν
Bulk modulus	K =			K
Shear modulus	G =		G	G	μ
Lamé parameter λ	λ =				λ
Lamé parameter μ	μ =		G	G	μ
Pressure- wave speed	cp =
Shear-wave speed	cs =

According to Table 3-1, the elasticity matrix D for isotropic materials is written in terms of Lamé parameters λ and μ,

or in terms of the bulk modulus K and shear modulus G:

There are two different ways to represent orthotropic or anisotropic data. The converts the indices as:

thus, Hooke’s law is presented in the form involving the elasticity matrix D and the following vectors:

COMSOL Multiphysics uses the complete tensor representation internally to perform the coordinate system transformations correctly.

Beside the , the elasticity coefficients can be entered following the notation. In the , the sorting of indices is:

The last three rows and columns in the elasticity matrix D are thus swapped.

The elasticity matrix for orthotropic materials in the has the following structure:

where the components are as follows:

where

The values of Ex, Ey, Ez, νxy, νyz, νxz, Gxy, Gyz, and Gxz are supplied in designated fields in the physics interface. COMSOL Multiphysics deduces the remaining components — νyx, νzx, and νzy — using the fact that the matrices D and D−1 are symmetric. The compliance matrix has the following form:

	The values of νxy and νyx are different for an orthotropic material. For a certain set of given material data, you must make sure that the definition of the indices is consistent with the definition used in COMSOL Multiphysics.

The elasticity matrix in the changes the sorting of the last three elements in the elasticity matrix:

If a pair of elastic moduli is present in the material definition, the values of Ex, Ey, Ez, νxy, νyz, νxz, Gxy, Gyz, and Gxz are computed automatically. Note that the resulting elasticity matrix will be isotropic. Depending on which pair of elastic moduli that is available, the expressions in Table 3-1 are used to find the above values.

In the general case of fully anisotropic material, you provide explicitly all 21 components of the symmetric elasticity matrix D, in either or .

If a pair of elastic moduli is present in the material definition, the components of the symmetric elasticity matrix D are computed using one of Equation 3-13 to Equation 3-15. Depending on which pair of elastic moduli that is available, the expressions in Table 3-1 are used to compute the necessary values. In case the orthotropic properties Ei, νij, and Gij are present in the material definition, the components of the symmetric elasticity matrix D are computed using Equation 3-16. Note that the resulting elasticity matrix will not be fully anisotropic in neither case.

For the linear elastic material, the stress components in coordinate system are

For anisotropic and orthotropic materials, the 4th-order elasticity tensor is defined from D matrix according to:

The user input D matrix always contains the physical components of the elasticity tensor

and the corresponding tensor components are computed internally according to:

For an isotropic material:

where λ and μ are the first and second Lamé elastic parameters and g is the metric tensor.

For a hyperelastic material, the second Piola–Kirchhoff stress tensor is computed as

which is computed as the contravariant components of the stress in the local coordinate system:

The energy variation is computed as

which can be also written as

The free energy for the linear thermoelastic material can be written as

where the strain energy density Ws(ε, T) is given by Equation 3-12. Hence, the stress can be found as

and the entropy per unit volume can be calculated as

where T0 is a reference temperature, the volumetric heat capacity ρCp can be assumed to be independent of the temperature (Dulong–Petit law), and the elastic entropy is

where α is the thermal expansion coefficient tensor. For an isotropic material, it simplifies into

The heat balance equation can be written as

where k is the thermal conductivity matrix, and the heat source caused by the dissipation is

where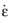

is the strain-rate tensor and the tensor τ represents all possible inelastic stresses (for example, a viscous stress).

Using the tensor components, the heat balance can be rewritten as:

In many cases, the second term can be neglected in the left-hand side of Equation 3-17 because all Tαmn are small. The resulting approximation is often called uncoupled thermoelasticity.

In case of geometric linearity, the governing equations for a linear elastic medium of any anisotropy can be written in terms of the structural displacement vector u as:

where C is the elasticity tensor.

Since the equations are linear, they possess the following time-harmonic wave solutions:

where k = kn is the wave number vector, and n is the direction vector that defines the wavefront propagation direction. The wavefront is an imaginary line connecting solid particles of the same phase. The velocity of such wavefront in the direction normal to it is given by the phase velocity c = ω/k.

Using such a wave solution form leads to Christoffel’s equation:

where the Christoffel’s tensor is defined as

The Christoffel’s equation can be considered as an eigenvalue problem. Thus, to have a nontrivial solution un, the phase velocity must satisfy

which is often called the dispersion relation. In a general case, this is a cubic polynomial with three roots

. Thus, for an arbitrary anisotropic medium, three waves with different phase velocities can propagate in each given direction.

If the wave propagation is initiated by a small perturbation that is initially localized in space, the solution can be found using the Fourier and Laplace transforms, and it will represent a so-called wave packet. The wave packet will propagate with the group velocity given by:

where un,j is the wave polarization vector that is the eigenvector corresponding to the eigenvalue solution

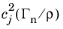
of Christoffel’s equation.

COMSOL Multiphysics provides predefined variables for the phase and group velocities for waves of different types propagating in any chosen direction. These variables do not affect the solution as such, but are available during result presentation if the Wave Speeds node has been added to the material.