Double Gauss Lens — Parametric Sweep

In the tree, select .

Parameters 1: Lens Prescription

Global Definitions

In the window, under click .

In the window for , type Parameters 1: Lens Prescription in the text field.

. The lens prescription will be added when the geometry sequence is inserted in the following section.

Parameters 2: General

The Double Gauss Lens Parametric simulation parameters can be loaded from a text file.

In the toolbar, click

and choose .

In the window for , type Parameters 2: General in the text field.

Locate the section. Click

Browse to the model’s Application Libraries folder and double-click the file double_gauss_lens_parametric_parameters.txt.

Component 1 (comp1)

In the window, click .

In the window for , locate the section.

Find the subsection. From the list, choose . The ray tracing algorithm used by the Geometrical Optics interface computes the refracted ray direction based on a discretized geometry via the underlying finite element mesh. A cubic geometry shape order usually introduces less discretization error compared to the default, which uses linear and quadratic polynomials.

Definitions

Load the variable definitions from a text file. These variables are used during postprocessing of the results. Note that the withsol variables have been defined to reflect the range of the parametric sweep.

Variables 1

In the window, expand the node.

Right-click and choose .

In the window for , locate the section.

Insert the prepared geometry sequence from file. You can read the instructions for creating the geometry in the appendix. Following insertion, the lens definitions will be available in the node.

Browse to the model’s Application Libraries folder and double-click the file double_gauss_lens_parametric_variables.txt.

Double Gauss Lens

In the window, under click .

In the window for , type Double Gauss Lens in the text field.

In the toolbar, click

Browse to the model’s Application Libraries folder and double-click the file double_gauss_lens_geom_sequence.mph.

In the toolbar, click

button in the toolbar. Orient the view to place the z-axis (optical axis) horizontal and the y-axis vertical.

The following variables are not needed to trace the rays but may be useful during postprocessing.

button in the toolbar. Compare the resulting geometry to Figure 2.

Add Material

In the toolbar, click

to open the window.

Go to the window.

In the tree, select .

Click in the window toolbar.

In the tree, select .

Click in the window toolbar.

In the tree, select .

Click in the window toolbar.

In the toolbar, click

to close the window.

Materials

Hoya LAF3 (mat1)

In the window, under click .

In the window for , locate the section.

From the list, choose . Each of the 6 lenses has been assigned to one of three lens material selections.

Hoya BAF11 (mat2)

In the window, click .

In the window for , locate the section.

From the list, choose .

Schott N-SF5 (mat3)

In the window, click .

In the window for , locate the section.

From the list, choose .

Geometrical Optics (gop)

In the window, under click .

In the window for , locate the section.

In the text field, type 0. In this simulation stray light is not being traced, so reflected rays will not be produced at the lens surfaces.

Select the check box. In this simulation, the geometry normals are used to apply the boundary conditions on all refracting surfaces. This is appropriate for the highest accuracy ray traces in single-physics simulations, where the geometry is not deformed.

Locate the section. Select the check box.

Select the check box.

Medium Properties 1

In the window, under click .

In the window for , locate the section.

From the list, choose . Each of the materials added above contain the optical dispersion coefficients which can be used to compute the refractive index as a function of wavelength.

Material Discontinuity 1

In the window, click .

In the window for , locate the section.

From the list, choose .

Ray Properties 1

In the window, click .

In the window for , locate the section.

In the λ0 text field, type lam_vac. This wavelength was defined in the node. It will be updated during the .

Release from Grid 1

Release the rays from a hexapolar grid, using quantities defined in the node.

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Specify the qc vector as


dx	x
dy	y
dz	z

The of the hexapolar grid will change according to the field angle.

Specify the rc vector as


nix	x
niy	y
niz	z

The is the same as the global optical axis.

In the Rc text field, type P_nom/2.

In the Nc text field, type N_ring.

Locate the section. Specify the L0 vector as


vx	x
vy	y
vz	z

The is calculated using the field angles defined in the node.

Obstructions

In the toolbar, click

and choose .

In the window for , type Obstructions in the text field.

Locate the section. From the list, choose .

Stop

In the toolbar, click

and choose .

In the window for , type Stop in the text field.

Locate the section. From the list, choose .

Image

In the toolbar, click

and choose .

In the window for , type Image in the text field.

Locate the section. From the list, choose . The default () will be used.

Mesh 1

In the window, under right-click and choose . The default physics-controlled mesh settings can be used in this simulation.

Study 1

In the following steps a parametric sweep study is constructed allowing the Double Gauss lens to be traced over multiple wavelengths and field angles.

In the window, click .

In the window for , locate the section.

Clear the check box. In this study, the plots will be created manually.

Clear the check box.

Parametric Sweep

In the toolbar, click

In the window for , locate the section.

From the list, choose .

In the table, enter the following settings:


Parameter name	Parameter value list	Parameter unit
lam_vac (Nominal vacuum wavelength)	range(lam_min,lam_step,lam_max)	nm
theta_y (Nominal Y field angle)	range(theta_y_min,theta_y_step,theta_y_max)	deg

Step 1: Ray Tracing

In the window, click .

In the window for , locate the section.

From the list, choose .

In the text field, type 0 200. The maximum optical path length is sufficient for rays released at large field angles to reach the image plane.

In the toolbar, click

Results

Create a plot showing the ray trajectories with color expressions, as well as a spot diagram in the image plane.

In the window, expand the node.

Ray 1

Create a dataset to use with the Ray Diagrams.

In the window, expand the node.

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Create a dataset to make image plane spot diagrams.

Image Plane

In the toolbar, click

In the window for , type Image Plane in the text field.

Locate the section. From the list, choose .

In the text field, type z_image.

In the following steps, a ray diagram is created showing all field angles and wavelengths and a custom color expression is added.

In the toolbar, click

In the window for , type Ray Diagram in the text field.

Click to expand the section. From the list, choose .

Locate the section. Clear the check box. The lenses will be rendered using a plot.

Mesh 1

Create a plot to render the lens elements as solids.

Right-click and choose .

In the window for , click to expand the section.

Locate the section. From the list, choose .

From the list, choose .

Add plots to show the stop and image plane.

Surface 1

In the window, right-click and choose .

In the window for , locate the section.

From the list, choose .

Locate the section. From the list, choose .

From the list, choose .

Selection 1

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Surface 2

In the window, under right-click and choose .

Selection 1

In the window, expand the node, then click .

In the window for , locate the section.

From the list, choose .

Color the rays according to the normalized radial distance from the centroid.

In the window, click .

Ray Trajectories 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Click to expand the section. From the list, choose .

Color Expression 1

Right-click and choose .

In the window for , locate the section.

In the text field, type at('last',gop.rall/gop.rmaxall).

Filter 1

In the window, right-click and choose .

Select only rays that reach the image plane; i.e., the final ray status (fs) is 2 (frozen).

In the window for , locate the section.

From the list, choose .

In the text field, type gop.fs==2.

Ray Trajectories 1

For all other wavelength and field angles, the details used for the first wavelength and field angle can be duplicated.

Ray Trajectories 2

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Click to expand the section. From the list, choose . This step only needs to be taken on the first duplication.

Ray Trajectories 3

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Ray Trajectories 4

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Ray Trajectories 5

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Ray Trajectories 6

Right-click and choose .

In the window for , locate the section.

From the list, choose .

Spot Diagrams

In the following steps, image plane spot diagrams for each field angle are created, and custom color expressions are added.

First, create a spot diagram for the on-axis field.

Spot Diagram 1

In the toolbar, click

and choose .

In the window for , type Spot Diagram 1 in the text field.

Click to expand the section. From the list, choose .

Locate the section. Select the check box.

In the associated text field, type X-axis.

Select the check box.

In the associated text field, type Y-axis.

Locate the section. Select the check box.

Poincaré Map 1

In the toolbar, click

and choose .

In the window for , locate the section.

From the list, choose .

Color Expression 1

Right-click and choose .

In the window for , locate the section.

In the text field, type lam_vac.

From the list, choose .

Click to expand the section. Select the check box.

In the text field, type 375.

In the text field, type 725.

Locate the section. From the list, choose .

Poincaré Map 2

In the window, under right-click and choose .

In the window for , locate the section.

From the list, choose .

Click to expand the section. From the list, choose .

Poincaré Map 3

Right-click and choose .

In the window for , locate the section.

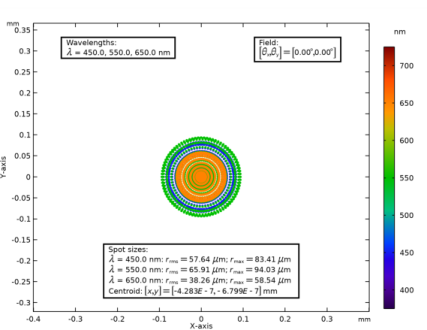
From the list, choose .

Annotation 1

In the window, right-click and choose .

In the window for , locate the section.

From the list, choose .

Locate the section. In the text field, type Wavelengths: \\ $\lambda$ = eval(lam1/1[nm]), eval(lam2/1[nm]), eval(lam3/1[nm]) nm.

Select the check box.

From the list, choose .

Locate the section. In the text field, type qx_ave0-1.5*r_max.

In the text field, type qy_ave0+1.5*r_max.

Click to expand the section. In the text field, type 4.

Locate the section. Select the check box.

Clear the check box.

Select the check box.

Annotation 2

Right-click and choose .

In the window for , locate the section.

In the text field, type Field: \\ $\left[\theta_\textrm{x},\theta_\textrm{y}\right] = \left[eval(theta_x0/1[deg])^\circ,eval(theta_y0/1[deg])^\circ\right]$.

Locate the section. In the text field, type qx_ave0+1.5*r_max.

Locate the section. In the text field, type 3.

Locate the section. From the list, choose .

Annotation 3

Right-click and choose .

In the window for , locate the section.

In the text field, type Spot sizes: \\ $\lambda$ = eval(lam1/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms0_1)~\mu$m; $r_\textrm{max} = eval(r_max0_1/1[um])~\mu$m \\ $\lambda$ = eval(lam2/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms0_2)~\mu$m; $r_\textrm{max} = eval(r_max0_2/1[um])~\mu$m \\ $\lambda$ = eval(lam3/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms0_3)~\mu$m; $r_\textrm{max} = eval(r_max0_3/1[um])~\mu$m \\ Centroid: $[x,y] = [eval(qx_ave0),eval(qy_ave0)]$ mm.

Locate the section. In the text field, type qx_ave0.

In the text field, type qy_ave0-1.30*r_max.

Locate the section. In the text field, type 4.

Locate the section. From the list, choose .

In the toolbar, click

Now, create a spot diagram for the off-axis field.

button in the toolbar. Compare the plot to Figure 4.

Spot Diagram 2

In the window, right-click and choose .

In the window for , type Spot Diagram 2 in the text field.

Poincaré Map 1

In the window, expand the node, then click .

In the window for , locate the section.

From the list, choose .

Poincaré Map 2

In the window, click .

In the window for , locate the section.

From the list, choose .

Poincaré Map 3

In the window, click .

In the window for , locate the section.

From the list, choose .

Annotation 1

In the window, click .

In the window for , locate the section.

In the text field, type qx_ave1-1.5*r_max.

In the text field, type qy_ave1+1.5*r_max.

Annotation 2

In the window, click .

In the window for , locate the section.

In the text field, type Field: \\ $\left[\theta_\textrm{x},\theta_\textrm{y}\right] = \left[eval(theta_x1/1[deg])^\circ,eval(theta_y1/1[deg])^\circ\right]$.

Locate the section. In the text field, type qx_ave1+1.5*r_max.

In the text field, type qy_ave1+1.5*r_max.

Annotation 3

In the window, click .

In the window for , locate the section.

In the text field, type Spot sizes: \\ $\lambda$ = eval(lam1/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms1_1)~\mu$m; $r_\textrm{max} = eval(r_max1_1/1[um])~\mu$m \\ $\lambda$ = eval(lam2/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms1_2)~\mu$m; $r_\textrm{max} = eval(r_max1_2/1[um])~\mu$m \\ $\lambda$ = eval(lam3/1[nm]) nm: $r_\textrm{rms} = eval(1e3*r_rms1_3)~\mu$m; $r_\textrm{max} = eval(r_max1_3/1[um])~\mu$m \\ Centroid: $[x,y] = [eval(qx_ave1),eval(qy_ave1)]$ mm.

Locate the section. In the text field, type qx_ave1.

In the text field, type qy_ave1-1.30*r_max.

In the toolbar, click