PDF
Thermally Induced Creep
Introduction
This example computes the stress history over a very long time for a material that exhibits creep behavior. The model is taken from NAFEMS Selected Benchmarks For Material Non-Linearity, Volume 2 (Ref. 1). The displacement and stress levels are compared with the values given in the reference.
Model Definition
The geometry is a hollow sphere with an inner radius of 200 mm and an outer radius of 500 mm. The problem has rotational symmetry where the solution depends only on the radial coordinate. You could therefore select any section having radial cuts as the computational domain. To follow the original example the sphere is modeled with a 2D axisymmetric 10° sector with symmetry constraint conditions applied on edges of the sector; see Figure 1.
Figure 1: The model geometry, using a 10° sector of the original geometry.
Material Properties
•
Isotropic with E = 10 GPa, ν = 0.25.
•
Creep data according to:
(1)
with A1 = 3.0·10-6 h-1 that accounts for the stress normalization of the equivalent stress, σe, in MPa, n1 = 5.5, and f2(T) = e−12500/T, where T defines the temperature in K .
Loads
•
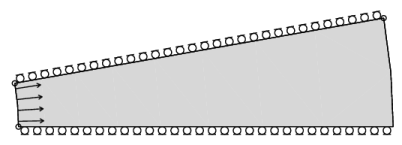
An internal pressure of 30 MPa.
•
A temperature field with the distribution where R and Z are material coordinates in mm.
Results and Discussion
The evolution of the displacement with time is shown in Figure 2. The upper curve represents the inner radius, and the lower curve represents the outer radius.
Figure 2: Radial displacement at the inner radius and the outer radius.
In the following table you can compare the values at time 1010 h with the reference values:
Radius
COMSOL Multiphysics
Reference (Ref. 1)
200 mm
26.0 mm
26.1 mm
500 mm
4.20 mm
4.22 mm
Initially the mechanical and thermal load have greater influence on the inner boundary of the sphere and results in larger creep strains. This with time causes relaxation that propagates from the inner radius toward the outer radius. This phenomena is visible in Figure 3 where the von Mises stress is shown at 108 h
.
Figure 3: Distribution of von Mises equivalent stress at t = 108 h.
Figure 3 shows the variation of von Mises stress with time at the inner, middle, and outer radii. Notice that significant changes in the stress state occur already at the time 104 h — that is, after one millionth of the total analysis time. In the final state, the stresses are completely redistributed. The mechanical load is then larger on the outer exterior than the inner exterior.
Figure 4: History of the von Mises stress at r = 205 mm, 350 mm, and 495 mm.
The following table shows the final values of the von Mises stress at t = 1010 h and the reference values for comparison:
radius
COMSOL Multiphysics
Reference (Ref. 1)
205 mm
11.4 MPa
11.5 MPa
350 mm
17.6 MPa
17.6 MPa
495 mm
21.1 MPa
21.1 MPa
Notes About the COMSOL Implementation
An interesting feature of creep problems is the extreme variation in the time scales over which different phenomena occur. Figure 4 shows that a significant change in stress starts after about 1000 h. It is therefore wise to solve for time steps before and after any significant change in the response. To capture this onset of the stress change, a strict time stepping is used, which forces the solver to provide a solution for all specified time steps. Alternative ways is to either provide an analytical solution for the inner pressure as initial conditions, or to first solve a stationary problem with the inner pressure followed by a time-dependent study.
The creep law defined in Equation 1 follows Norton law, which is available in the Nonlinear Structural Materials Module. In COMSOL Multiphysics it is defined as
In order to normalize the equivalent stress in MPa, set the reference stress σr = 1 MPa. In the exponential temperature function R = 8.314 J/(mol·K) and therefore the creep activation energy Q = 1.039·105 J/mol.
Reference
1. D. Linkens, Selected Benchmarks For Material Non-Linearity, vol 2, NAFEMS, 1993.
Application Library path: Nonlinear_Structural_Materials_Module/Creep/thermally_induced_creep
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D Axisymmetric.
2
In the Select Physics tree, select Structural Mechanics>Solid Mechanics (solid).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Time Dependent.
6
Click  Done.
Definitions
Variables 1
1
In the Home toolbar, click  Variables and choose Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
T
333[K]*(1+0.1[m]/sqrt(R*R+Z*Z))
K
Prescribed temperature field
Geometry 1
Circle 1 (c1)
1
In the Geometry toolbar, click  Circle.
2
In the Settings window for Circle, locate the Size and Shape section.
3
In the Radius text field, type 0.5.
4
In the Sector angle text field, type 10.
5
Click  Build All Objects.
6
Click the  Zoom Extents button in the Graphics toolbar.
Circle 2 (c2)
1
In the Geometry toolbar, click  Circle.
2
In the Settings window for Circle, locate the Size and Shape section.
3
In the Radius text field, type 0.2.
4
In the Sector angle text field, type 10.
5
Click  Build All Objects.
Difference 1 (dif1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the object c1 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Select the  Activate Selection toggle button.
5
Select the object c2 only.
6
Click  Build All Objects.
7
Click the  Zoom Extents button in the Graphics toolbar.
Solid Mechanics (solid)
Linear Elastic Material 1
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Linear Elastic Material 1.
Creep 1
1
In the Physics toolbar, click  Attributes and choose Creep.
2
In the Settings window for Creep, locate the Model Input section.
3
From the T list, choose User defined. In the associated text field, type T.
4
Locate the Creep Data section. Select the Include temperature dependency check box.
5
In the Q text field, type 1.0393e5[J/mol].
To enforce a symmetry constraint, add a Roller node.
Roller 1
1
In the Physics toolbar, click  Boundaries and choose Roller.
2
Select Boundaries 1 and 2 only.
Boundary Load 1
1
In the Physics toolbar, click  Boundaries and choose Boundary Load.
2
Select Boundary 3 only.
3
In the Settings window for Boundary Load, locate the Coordinate System Selection section.
4
From the Coordinate system list, choose Boundary System 1 (sys1).
5
Locate the Force section. Specify the FA vector as
0
t1
-30[MPa]
n
6
In the Model Builder window, click Solid Mechanics (solid).
7
In the Settings window for Solid Mechanics, locate the Structural Transient Behavior section.
8
From the list, choose Quasistatic.
Materials
Material 1 (mat1)
1
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Young’s modulus
E
10[GPa]
Pa
Basic
Poisson’s ratio
nu
0.25
1
Basic
Density
rho
1000
kg/m³
Basic
Creep rate coefficient
A_nor
3e-6[1/h]
1/s
Norton
Reference stress
sigRef_nor
1[MPa]
N/m²
Norton
Stress exponent
n_nor
5.5
1
Norton
Mesh 1
Mapped 1
In the Mesh toolbar, click  Mapped.
Size
1
In the Model Builder window, click Size.
2
In the Settings window for Size, locate the Element Size section.
3
From the Predefined list, choose Coarse.
4
Click  Build All.
Study 1
Step 1: Time Dependent
1
In the Model Builder window, under Study 1 click Step 1: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
From the Time unit list, choose h.
4
In the Output times text field, type 0.
5
Click  Range.
6
In the Range dialog box, type 0 in the Start text field.
7
In the Stop text field, type 10.
8
In the Step text field, type 0.2.
9
From the Function to apply to all values list, choose exp10(x) – Exponential function (base 10).
10
Click Add.
11
In the Settings window for Time Dependent, locate the Study Settings section.
12
From the Tolerance list, choose User controlled.
13
In the Relative tolerance text field, type 1e-4.
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 1 (sol1) node, then click Time-Dependent Solver 1.
3
In the Settings window for Time-Dependent Solver, click to expand the Time Stepping section.
4
From the Steps taken by solver list, choose Strict.
5
Select the Initial step check box.
6
In the associated text field, type 1[min].
Setting the initial step ensures an accurate calculation of the creep strain at t = 0.
7
Click  Compute.
Results
Stress (solid)
Select the solution at 108 hours to reproduce Figure 3.
1
In the Settings window for 2D Plot Group, locate the Data section.
2
From the Time (h) list, choose 1E8.
Surface 1
1
In the Model Builder window, expand the Stress (solid) node, then click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
From the Unit list, choose MPa.
4
In the Stress (solid) toolbar, click  Plot.
5
Click the  Zoom Extents button in the Graphics toolbar.
Surface 1
1
In the Model Builder window, expand the Results>Stress, 3D (solid) node, then click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
From the Unit list, choose MPa.
Follow the commands below to generate Figure 2.
Radial Displacement
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Radial Displacement in the Label text field.
3
Locate the Axis section. Select the x-axis log scale check box.
Point Graph 1
1
Right-click Radial Displacement and choose Point Graph.
2
Select Points 2 and 4 only.
3
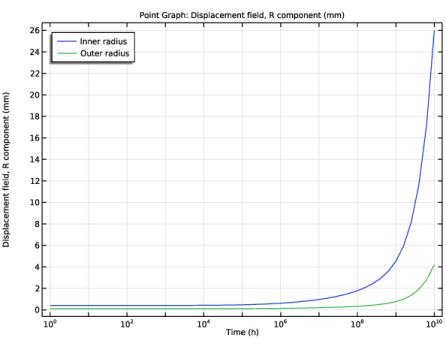
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Displacement>Displacement field - m>u - Displacement field, R component.
4
Locate the y-Axis Data section. From the Unit list, choose mm.
5
Click to expand the Legends section. Select the Show legends check box.
6
From the Legends list, choose Manual.
7
In the table, enter the following settings:
Legends
Inner radius
Outer radius
Radial Displacement
1
In the Model Builder window, click Radial Displacement.
2
In the Settings window for 1D Plot Group, locate the Legend section.
3
From the Position list, choose Upper left.
4
In the Radial Displacement toolbar, click  Plot.
The commands below generate Figure 4.
Cut Point 2D 1
1
In the Results toolbar, click  Cut Point 2D.
2
In the Settings window for Cut Point 2D, locate the Point Data section.
3
In the R text field, type 205[mm] 350[mm] 495[mm].
4
In the Z text field, type 0.
von Mises Stress
1
In the Results toolbar, click  1D Plot Group.
2
In the Settings window for 1D Plot Group, type von†Mises Stress in the Label text field.
3
Locate the Data section. From the Dataset list, choose Cut Point 2D 1.
4
Locate the Axis section. Select the x-axis log scale check box.
Point Graph 1
1
Right-click von Mises Stress and choose Point Graph.
2
In the Settings window for Point Graph, click Replace Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Solid Mechanics>Stress (Gauss points)>solid.misesGp - von Mises stress, Gauss point evaluation - N/m².
3
Locate the y-Axis Data section. From the Unit list, choose MPa.
4
Locate the Legends section. Select the Show legends check box.
5
From the Legends list, choose Manual.
6
In the table, enter the following settings:
Legends
r=205mm
r=350mm
r=495mm
7
In the von†Mises Stress toolbar, click  Plot.