
|

|
200 μm
|
170 μm
|
10 μm
|
146 μm
|
250 μm
|
|
|
2 μm
|
2 μm
|
2 μm
|
2 μm
|
120 μm
|
|
|
2.25 μm
|
2.25 μm
|
2.25 μm
|
2.25 μm
|
2.25 μm
|
|
|
T0
|
605oC
|
|
T1
|
25oC
|

|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file residual_stress_resonator_2d_parameters.txt.
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file residual_stress_resonator_2d_geom_sequence.mph.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Find the Expression for remaining selection subsection. In the Volume reference temperature text field, type T1.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file residual_stress_resonator_2d_geom_sequence.mph.
|
|
3
|
In the Insert Sequence from File dialog box, select Geometry 2 in the Select geometry sequence to insert list.
|
|
4
|
Click OK.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
In the Model Builder window, under Component 2 (comp2) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Paste Selection dialog box, type 4,8,10,11,28,30,38,42,44,45,60,62 in the Selection text field.
|
|
5
|
Click OK.
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Rename Study dialog box, type Study 1 - Straight Cantilever, No Stress in the New label text field.
|
|
3
|
Click OK.
|
|
1
|
In the Model Builder window, under Study 1 - Straight Cantilever, No Stress click Step 1: Eigenfrequency.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Rename Study dialog box, type Study 2 - Folded Cantilever, No Stress in the New label text field.
|
|
5
|
Click OK.
|
|
1
|
|
2
|
|
3
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Eigenfrequency, Prestressed.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Rename Study dialog box, type Study 3 - Straight Cantilever, Residual Stress in the New label text field.
|
|
6
|
Click OK.
|
|
1
|
|
2
|
|
3
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Eigenfrequency, Prestressed.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Rename Study dialog box, type Study 4 - Folded Cantilever, Residual Stress in the New label text field.
|
|
6
|
Click OK.
|
|
1
|
|
2
|
In the Rename 2D Plot Group dialog box, type Straight Cantilever, No Stress in the New label text field.
|
|
3
|
Click OK.
|
|
4
|
|
1
|
|
2
|
In the Rename 2D Plot Group dialog box, type Folded Cantilever, No Stress in the New label text field.
|
|
3
|
Click OK.
|
|
4
|
|
1
|
|
2
|
In the Rename 2D Plot Group dialog box, type Straight Cantilever, Residual Stress in the New label text field.
|
|
3
|
Click OK.
|
|
4
|
|
1
|
|
2
|
In the Rename 2D Plot Group dialog box, type Folded Cantilever, Residual Stress in the New label text field.
|
|
3
|
Click OK.
|
|
4
|
|
1
|
|
2
|
|
3
|
In the Rename 2D Plot Group dialog box, type Residual Stress in Straight Cantilever in the New label text field.
|
|
4
|
Click OK.
|
|
5
|
|
6
|
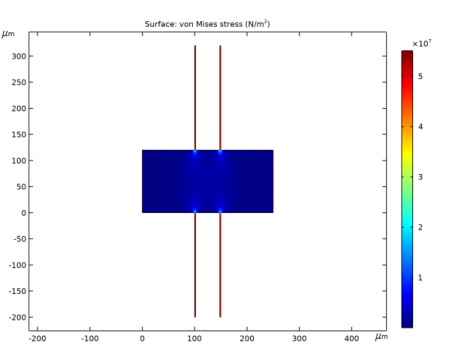
From the Dataset list, choose Study 3 - Straight Cantilever, Residual Stress/Solution Store 1 (7) (sol4).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
In the Rename 2D Plot Group dialog box, type Residual Stress in Folded Cantilever in the New label text field.
|
|
4
|
Click OK.
|
|
5
|
|
6
|
From the Dataset list, choose Study 4 - Folded Cantilever, Residual Stress/Solution Store 2 (12) (sol6).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
Select the object r2 only.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|