
|

|
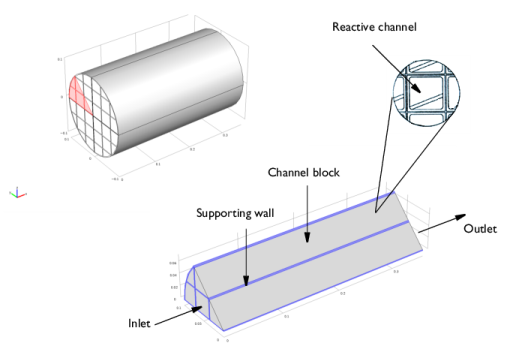
1
|
|
2
|
From the Application Libraries root, browse to the folder Chemical_Reaction_Engineering_Module/Tutorials and double-click the file monolith_kinetics.mph.
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, expand the Component 1 (comp1)>Reaction Engineering (re) node, then click Species: N2.
|
|
2
|
|
3
|
From the list, choose Solvent.
|
|
1
|
|
2
|
|
3
|
Find the Chemical species transport subsection. From the list, choose Transport of Diluted Species in Porous Media: New.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file monolith_3d_geom_sequence.mph.
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
Click Next in the window toolbar.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click Next in the window toolbar.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click Next in the window toolbar.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click Finish in the window toolbar.
|
|
1
|
In the Model Builder window, expand the Global Definitions>Materials node, then click Gas: ammonia(0)-nitrogen(1)-nitrogen oxide(0)-oxygen(0)-water(0) 1 (pp1mat1).
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click
|
|
7
|
|
8
|
Click OK.
|
|
9
|
|
10
|
|
11
|
|
12
|
Click
|
|
13
|
|
14
|
Click OK.
|
|
15
|
|
16
|
|
17
|
|
18
|
Click
|
|
19
|
|
20
|
Click OK.
|
|
21
|
|
23
|
|
24
|
|
25
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under 3D Model (comp2) click Transport of Diluted Species in Porous Media (tds).
|
|
2
|
In the Settings window for Transport of Diluted Species in Porous Media, locate the Domain Selection section.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
From the list, choose Diagonal.
|
|
6
|
|
7
|
From the list, choose Diagonal.
|
|
8
|
|
9
|
From the list, choose Diagonal.
|
|
10
|
|
11
|
From the list, choose Diagonal.
|
|
12
|
|
13
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
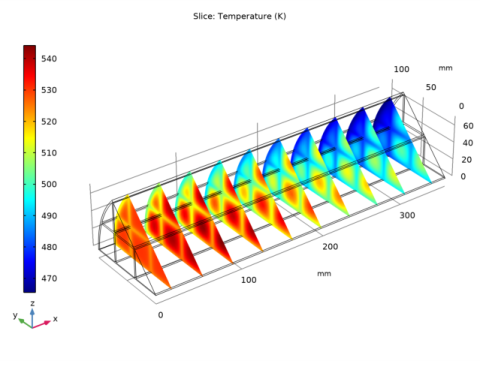
Locate the Heat Conduction, Porous Matrix section. From the ks list, choose User defined. From the list, choose Diagonal.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Darcy’s Law 1 (dl) node, then click Fluid and Matrix Properties 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Locate the Matrix Properties section. From the Porous material list, choose Solid: Monolith Material (mat1).
|
|
7
|
|
8
|
|
9
|
In the κ table, enter the following settings:
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
7
|
|
9
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Select the Description check box.
|
|
5
|
|
6
|
Click
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
Click Replace.
|
|
12
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
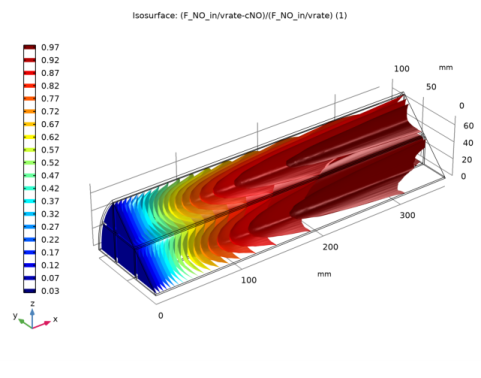
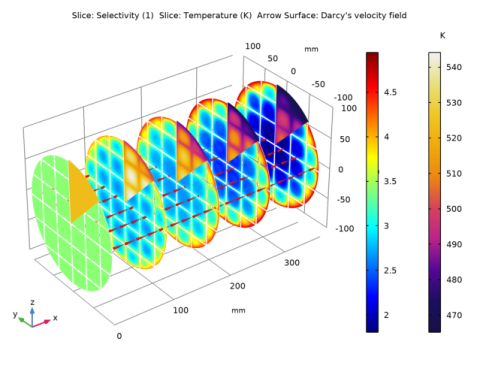
Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose 3D Model (comp2)>Darcy’s Law 1>Velocity and pressure>dl.u,dl.v,dl.w - Darcy’s velocity field.
|
|
5
|
|
6
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|