
|
|
1
|
|
2
|
In the Select Physics tree, select AC/DC>Electromagnetic Fields>Vector Formulations>Magnetic and Electric Fields (mef).
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
Click Browse.
|
|
4
|
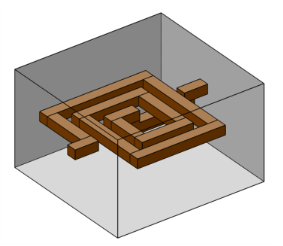
Browse to the model’s Application Libraries folder and double-click the file spiral_inductor.mphbin.
|
|
5
|
Click Import.
|
|
6
|
|
1
|
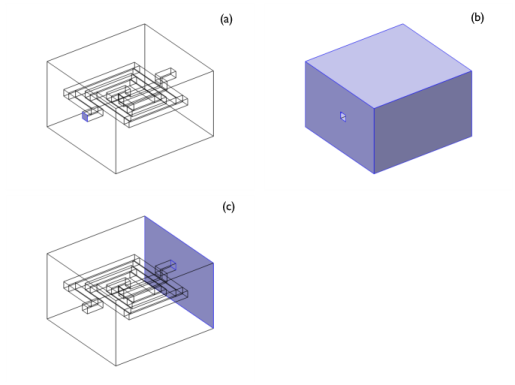
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
4
|
Click OK.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Click OK.
|
|
6
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
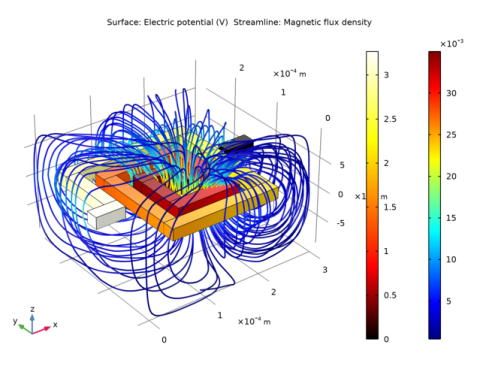
Locate the Coloring and Style section. Find the Line style subsection. From the Type list, choose Tube.
|
|
6
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
In the Settings window for Color Expression, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Magnetic and Electric Fields>Magnetic>mef.normB - Magnetic flux density norm - T.
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Magnetic and Electric Fields>Terminals>mef.L11 - Inductance - H.
|
|
3
|
Click
|
|
1
|
Go to the Table window.
|