You are viewing the documentation for an older COMSOL version. The latest version is
available here.
(2-132)

The pressure correction Δλv,P is calculated from the method of Stiel and Thodos, see
Ref. 32, which is applicable for
ρr<3, but is less accurate for H
2, strongly polar gases, and gases with a high degree of hydrogen bonding, such as H
2O and NH
3
(2-133)
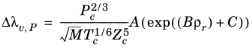
(2-134)

(2-135)

(2-136)
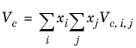
(2-137)
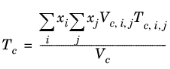
(2-138)
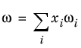
(2-139)

(2-140)
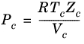
(2-141)
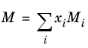
(2-142)
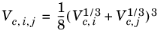
(2-143)
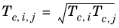
However, in order to ensure 0th-order continuity at
ρr = 0.5 and
ρr = 2.0, the following coefficients for
0.5 ≤ ρr < 2.0 are recalculated from
(2-144)

(2-145)
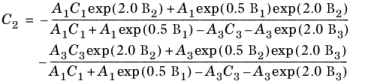
The vapor thermal conductivity correlation must be available for all species. Also critical volumes, Vc,i, critical temperatures,
Tc,i, molecular weights
Mi, and acentric factors
ωi must be specified for all species.
Lindsay and Bromley (see Ref. 34) provided an equation for the interaction parameters of the method of Wassiljewa (see
Ref. 35) based on the kinetic theory, to provide mixture thermal conductivity from pure species values
(2-146)
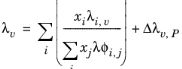
(2-147)
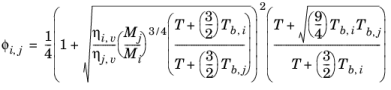
where the pressure correction Δλv,P is calculated from
Equation 2-133. Both vapor thermal conductivity correlation
λi,v and the vapor viscosity correlation
ηi,v must be available for all species. In addition, all normal boiling points
Ti,b, molecular weights
Mi, critical volumes
Vc,i, critical temperatures
Tc,i, and acentric factors
ωi must be specified.
(2-148)
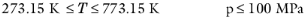
(2-149)
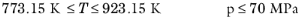
(2-150)

To calculate the mixture liquid thermal conductivity, λl,m, the values of pure liquid thermal conductivity correlations are mixed ideally
(2-151)

(2-152)
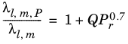
(2-153)
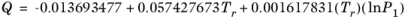
(2-154)

(2-155)
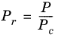
(2-156)
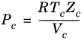
(2-157)
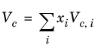
(2-158)
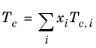
(2-159)
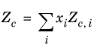
All liquid thermal conductivity correlations must be specified. All values for critical temperatures, Tc,i, critical volumes,
Pc,i and critical compressibility factors,
Zc,i must be specified for all species
i.
(2-160)
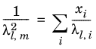
(2-161)
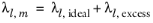
(2-162)
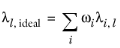
(2-163)
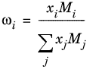
(2-164)
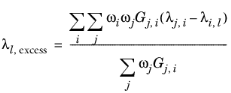
where Gj,i follows from
Equation 2-57. The binary interaction terms follow from
(2-165)
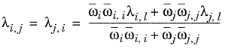
(2-166)
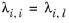
(2-167)
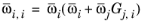
with ϖi is the composition in the binary mixture of species
i and
j and the local composition is equi-molar
(2-168)
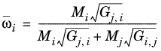
All liquid thermal conductivity correlations must be specified. The pressure dependence is introduced using Equation 2-152 –
Equation 2-159. All values for critical temperatures
Tc,i, critical volumes
Pc,i, critical compressibility factors
Zc,i, and molecular weights
Mi must be specified for all compounds
i. In addition, all NRTL binary interaction parameters
Ai,j must be specified. Unspecified values for NRTL interaction parameters
Bi,j are set to zero. The randomness parameters
αi,j have values of zero on the diagonal and the matrix is symmetric. All off-diagonal values must be specified. NRTL model is presented in
Equation 2-53 to
Equation 2-64.
Rowley (Ref. 53) adapted the local composition model by replacing the mixing rule in
Equation 2-165 by the following
(2-169)
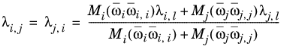
(2-170)

(2-171)
(2-172)
Wilke, see Ref. 37, based his method for mixture viscosity of the vapor phase on kinetic theory:
(2-173)
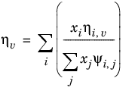
(2-174)
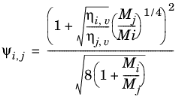
The vapor viscosity correlation ηi,v must be available for all species. In addition, all molecular weights
Mi must be specified.
Brokaw (see Ref. 38) uses the same basic equation as Wilke (
Equation 2-173). However,
Equation 2-174 is replaced by
(2-175)
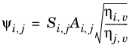
(2-176)
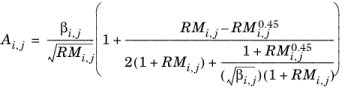
(2-177)
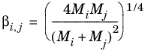 ,
, 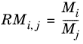
The vapor viscosity correlation, ηi,v must be available for all species
i. In addition, all molecular weights
Mi must be specified. If Lennard-Jones energy
εi (see
Ref. 39) Stockmayer’s polar parameter
δs,i(
Ref. 40 and
Ref. 41) are specified for both species
i and
j then
(2-178)

(2-179)
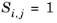
(2-180)
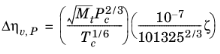
where ξ is calculated from the correlation of Jossi (
Ref. 42), which is applicable for
ρr < 3.0. It is less accurate for H
2, strongly polar gases and gases with a high degree of hydrogen bonding such as H
2O and NH
3.
(2-181)

(2-182)
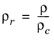
(2-183)
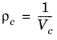
(2-185)
 ,
, 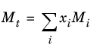
The values for critical volumes, Vc,i, critical temperatures,
Tc,i, critical compressibility factors,
Zc,i and molecular weights,
Mi must be specified for all species
i.
(2-186)
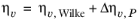
where ηv,Wilke is calculated from
Equation 2-173.
The corresponding states viscosity model of Pedersen (Ref. 43 and
Ref. 44) applies to both vapor and liquid phases of hydrocarbon mixtures. The selected reference species is CH
4.
The CH4 viscosity is calculated from
Ref. 45, modified by Pedersen and Fredunsland (
Ref. 46) to avoid issues below 91 K where CH
4 becomes solid
(2-187)
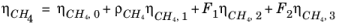
(2-188)
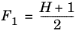
(2-189)
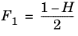
(2-190)
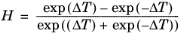
(2-191)

Here, ρCH4 is used in g/cm
3; for the mass-mole conversion of
ρCH4, a molecular weight of
MCH4 = 16.042568 g/mol is used.
(2-192)
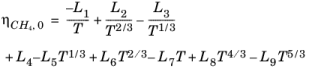
(2-193)
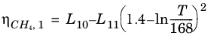
(2-194)
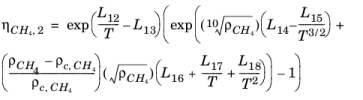
(2-195)
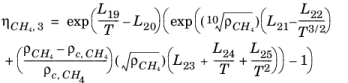
Here, ρCH4 is used in g/cm
3; the critical density is given by
ρc,CH4 = 0.16284 g/cm
3. The following equation by McCarty (
Ref. 47) is solved for the density of
CH4
(2-196)
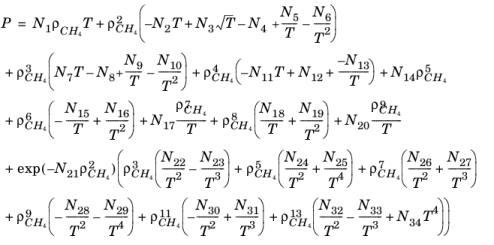
where ρCH4 is used in mol/l.
With the viscosity and density of CH4 defined, the viscosity of any mixture,
ηm, can be calculated from the corresponding states principle
(2-197)
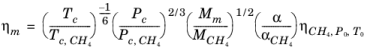
where CH4 viscosity
ρCH4,P0,T0 is calculated at temperature,
T0 and pressure
P0
(2-198)

(2-199)
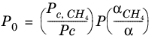
(2-200)
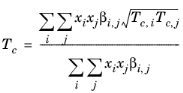
(2-201)
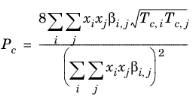
(2-202)
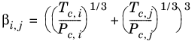
(2-203)
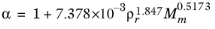
(2-204)
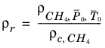
(2-205)
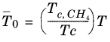
(2-206)
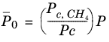
with ρc,CH4 = 0.16284 g/cm
3. For
CH4
(2-207)
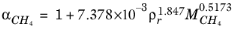
where Equation 2-204 is used. The mixture molecular weight is a function of the weight-averaged molecular weight and the number-averaged molecular weight
(2-208)
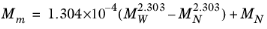
(2-209)

(2-210)

where the power in Equation 2-208 is determined by fitting to experimental viscosity data.
Note that pure species vapor viscosity correlations ηi,v are not required. However, for each species
i, molecular weight
Mi, critical temperature,
Tc,i and critical pressure,
Pc,i must be specified.
(2-211)
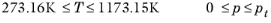
(2-212)
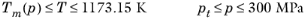
(2-213)

(2-214)

(2-215)

The values of pure species log liquid viscosity, ln ηi,l are mixed ideally using mole fractions
xi
(2-216)
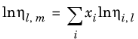
where ηm,l is the mixture viscosity of liquids.
(2-217)
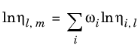
The Pedersen Corresponding States Model described above for the gas phase viscosity also applies to the liquid phase. Pure species liquid viscosity correlations are not required. However, for each species
i, molecular weight
Mi, critical temperature
Tc,i, and critical pressure
Pc,i, must be specified.
(2-218)
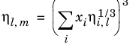
The model is noted in Ref. 51 to provide reasonable results for hydrocarbon mixtures of similar components.
(2-219)
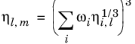
(2-220)

(2-221)
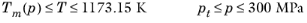
(2-222)

(2-223)

(2-224)

For dilute systems, the binary diffusion coefficient D0i,j represent the diffusivity of species
i in a medium consisting of pure species
j. This corresponds to the Fickian diffusion coefficient.
For any mixture, the binary Maxwell-Stefan diffusion coefficient 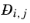 , represents the inverse drag coefficient of species i
, represents the inverse drag coefficient of species i moving past species
j (
Ref. 55 -
Ref. 58). This property is referred to as the Maxwell-Stefan diffusivity. The Maxwell-Stefan diffusivity is symmetric,
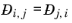
, and the diagonal elements
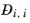
are not used. T
When the Gas diffusivity property model is set to Automatic, the Fuller Schettler Giddings model is used, provided that the Fuller diffusion volume is known for both species (
i and
j), otherwise the
Wilke-Lee model is used.
Fuller et al. (Ref. 59) modified the Chapman-Enskog relation to correlate binary diffusion coefficient for species
i and
j in the vapor phase according to the Fuller Schettler Giddings (FGS) model:
(2-225)

where T denotes the temperature (K),
Mi the molecular weight of species
i (g/mol
) and
P is the pressure
(Pa).
vi are the atomic diffusion volumes (Fuller diffusion volume),
(cm
3), which are estimated using group contribution for each species (
Ref. 60):
Wilke and Lee (Ref. 61) also modified the Chapman-Enskog relation to correlate binary diffusion coefficient in vapor phase according to:
(2-226)
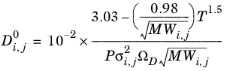
(2-227)
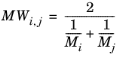
(2-228)

(2-229)
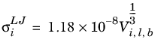
where Vi,l,b is the molar volume of species at normal boiling point.
(2-230)
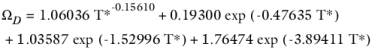
(2-231)
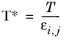
(2-232)
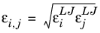
(2-233)
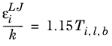
where k is the Boltzmann constant, and

is normal boiling point temperature.
(2-234)
All models for gas phase diffusion at infinite dilution are symmetric, the diffusivity of species i in species
j equals that of species
j in species
i. In addition, under the ideal gas assumption, the Maxwell-Stefan diffusion coefficient matches the Fick diffusion coefficient. This implies that the Maxwell-Stefan gas diffusivities provided are independent of composition.
When the Liquid diffusivity at infinite dilution property model is set to Automatic, a selection for each solute i in solvent
j will be made from the models according to the following rules. Except in the case of a temperature correlation and the
Erkey-Rodden-Akgerman model, all of these rules require that the log liquid viscosity correlation, ln
ηj is available in the database for species
j and that the liquid volume at normal boiling point,
Vi,l,b is available for the species
i.
|
•
|
If parachors Pi and Pj are both available, and the liquid volume at normal boiling point, Vi,l,b is available for the solvent, the Tyn-Calus correlation is used.
|
For the Siddiqi-Lucas method, a molecule is considered organic if it has at least one C atom bound to anything else than O or C atoms. This is determined by the SMILES formula, if available. If, for any pair of species, the required input data for none of the above models is available, the entire property liquid diffusion coefficient at infinite dilution is not available.
The correlation by Wilke and Chang (Ref. 63) for liquid phase diffusion coefficients at infinite dilution is:
(2-235)
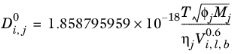
Molecular weight, Mj and log liquid viscosity correlation,

, for species
j and liquid molar volume at normal boiling point for species
i,
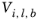
, is required. The Wilke-Chang association parameter
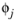
, if unavailable, is set to:
The Correlation by Tyn and Calus (Ref. 66) for liquid diffusion coefficients at infinite dilution reads:
(2-236)
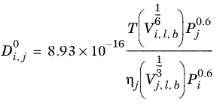
The log liquid viscosity correlation 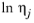 should be available for species j
should be available for species j, The liquid volume at normal boiling point,
Vi,l,b and parachor,
Pi should be available for both species
i and
j.
If the solute is water, both the liquid volume at normal boiling point, Vi,l,b and parachor,
Pi for the solute are corrected by a factor 2. This factor also applies if it is detected from the SMILE formula that the species is an organic acid (a carboxyl group is found), except in the cases where the solvent is water, methanol or n-butanol.
Hayduk and Minhas (Ref. 67) suggested three different correlations for liquid diffusion coefficients at infinite dilution.
Aqueous Solutions: in case the solvent is water (derived from CAS number or SMILES formula), the correlation reads:
(2-237)
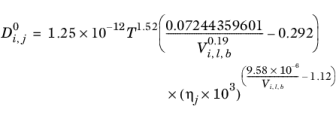
Normal paraffin solutions: In case both the solute and solvent are normal paraffins (derived from SMILES formula), the correlation reads:
(2-238)
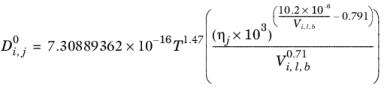
(2-239)
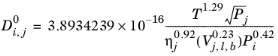
If the solute is water, both the liquid volume at normal boiling point, Vi,l,b and parachor,
Pi for solute are corrected by a factor 2. This factor also applies if it is detected from the SMILES formula that the species is an organic acid (a carboxyl group is found), except in the cases where the solvent is water, methanol or n-butanol.
Siddiqi and Lucas (Ref. 68) suggested correlations for liquid diffusion coefficients at infinite dilution for aqueous system (including gases) and for organic solutions. For normal paraffins systems, they recommended the
Hayduk-Minhas model.
(2-240)
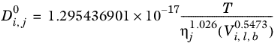
(2-241)
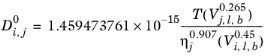
Where T is temperature, Vi,l,b is liquid volume at normal boiling point and
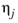
is the viscosity of the solvent.
The correlation by Erkey et al. (Ref. 69) for liquid diffusion coefficients at infinite dilution in normal paraffins is:
(2-242)

(2-243)
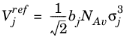
NAv is Avogadro’s number, and the deviation from closest packing volume is given by
(2-244)
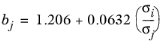
The correlation is fitted to normal paraffins, hydrogen, carbon monoxide and carbon dioxide diffusing in normal paraffins. The molecular weight Mi should be available for both solute and solvent. The Lennard-Jones diameter,
σi is estimated from Bondi group contribution method (
Ref. 70), and for some species are taken from
Ref. 69 and
Ref. 71 as:
(2-245)
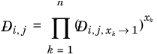
where 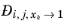 denotes the Maxwell-Stefan liquid diffusion coefficient for species i
denotes the Maxwell-Stefan liquid diffusion coefficient for species i and
j in the limited of pure species
k. If
k=
j, it represents a binary system of species
i and
j where
i is infinitely diluted. In addition, at infinite dilution the thermodynamics factor (activity) (
Ref. 58) becomes unity and the Maxwell-Stefan diffusivity equals to Fick diffusivity:
(2-246)
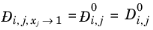
(2-247)
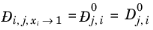
(2-248)
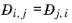
(2-249)
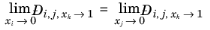
For binary systems, Equation 2-245 reduces to the Vignes interpolation formula.
(2-250)
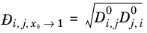
(2-251)
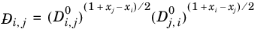
Kooijman and Taylor (Ref. 74) found on a limited number of systems that this provides better results:
(2-252)
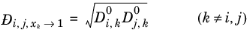
(2-253)

Wesselingh and Bollen (Ref. 75) asserted that this is a reasonable estimate.
Krishna and van Baten (Ref. 76), on the basis of data obtained from molecular dynamic simulations, proposed the following Vignes-based (
Ref. 72) interpolation:
(2-254)
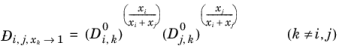
The model reduces to the Kooijman-Taylor model for
xi =
xj. The value of
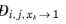
is undefined in the limit of both
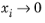
and

. From a physical point of view this is inconsequential as the value cancels out in the expressions obtained for the fluxes using the Maxwell-Stefan equations. Nevertheless, in order to obtain well-defined values and composition derivatives of
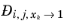
itself, the equation is modified to:
(2-255)
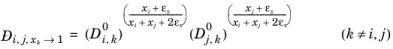
(2-256)
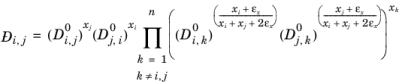
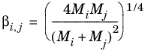 ,
,